e funktion punkte gegenemn

Question

e-funktion finden die durch die punkte durchläuft


f(x)=k*a^x   P(1/8) Q(3/128)
f(x) k*a^x   P(1/-6)     Q(4/-162)

Comments

Ich habe dir das unter
https://www.mathelounge.de/133990/funktion-f-finden-die-durch-die-punkte-16-und-q-4-256-verlauft

doch schon vorgemacht. versuche mal ob du das auch so machen kannst.

---

ich hab es versucht aber ich bekomme es immer was falsches raus

deswegen wollte ich euch bzw. dich fragen

---

Teil uns doch mal deine Rechnung mit. Dann können wir dir sagen wo du einen Fehler gemacht hast.

---

k*a^1=8

k*a^3=128

8*a^2=128

a=4


k*4^3=128

k=2


f(x)=4^x

---

f(x)=k*a^x

Wenn du für k = 2 und für a = 4 einsetzt wie du ausgerechnet hast bekommst du aber

f(x)=2*4^x

Answer 1

Hallo Aniththa,

 

Du setzt ganz einfach die beiden gegebenen Punkte in die Funktionsgleichung ein und erhältst so zwei Gleichungen mit den beiden Unbekannten k und a:

 

f(x)=k*a^x   P(1/8) Q(3/128)

I. 8 = k * a¹ | k = 8/a

II. 128 = k * a³

I in II eingesetzt:

128 = 8/a * a³ = 8a² | :8

16 = a² | Wurzel; aufpassen: 2 Werte!!

a_1,2 = ± 4

a₁ = 4 eingesetzt in I: k₁ = 2

a₂ = -4 eingesetzt in I: k₂ = -2

EDIT:

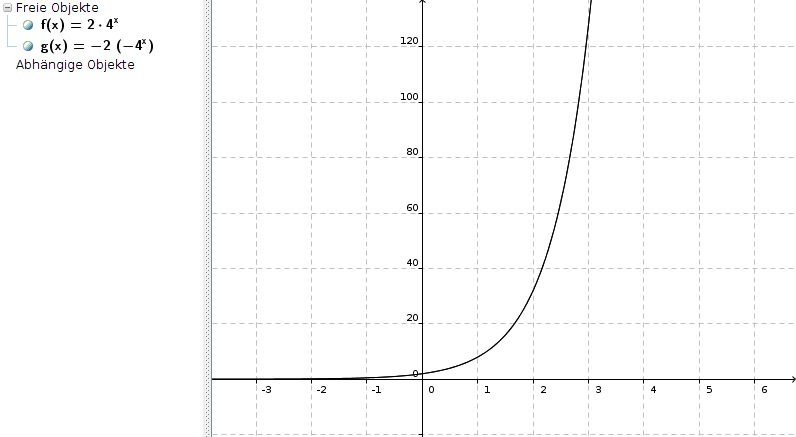
Siehe aber zur Funktionsgleichung g(x) = -2 * (-4)^x unbedingt die Kommentare vom Mathecoach!

Auf der sicheren - und richtigen - Seite ist man also nur mit der Funktion f(x) = 2 * 4^x

Deshalb bitte die Funktion g(x) ignorieren!!!

 

Probe:

8 = 2 * 4¹ | stimmt

8 = -2 * (-4)¹ | stimmt

 

f(x) = k*a^x   P(1/-6)     Q(4/-162)

I. -6 = k * a¹ | k = -6/a

II. -162 = k * a⁴

I in II eingesetzt

-162 = -6/a * a⁴ = -6a³ | : (-6)

27 = a³ | 3. Wurzel

a = 3

Eingesetzt in I:

k = -6/3 = -2

f(x) = -2 * 3^x

Probe:

-6 = -2 * 3¹ | stimmt

-162 = -2 * 3⁴ = -2 * 81 | stimmt

 

Besten Gruß

Comments

Die Potenzfunktion
g(x) = -2 * (-4)^x

ist meiner Meinung nach sehr ungünstig. Vielleicht weißt du auch warum?

---

@Aniththa:

Habe nach Hinweisen vom Mathecoach eine Korrektur vorgenommen - bitte unbedingt beachten!!

Answer 2

Hier die Ergebnisse zum Kontrollieren. Aber du solltest zunächst es selber versuchen.

f(x)=k*a^x   P(1/8) Q(3/128)

f(x) = 2 * 4^x

f(x) k*a^x   P(1/-6)     Q(4/-162)

f(x) = -2 * 3^x

Comments

bei der ersten aufgabe wie du oben siehst hab ich meine rechnungsschritte aufgeschrieben ich komme nicht auf deinen ergebis die 4 habe ich aber die 2 nicht  und 2*4 ist 8 und 8 hoch 3 ist nicht 128 sondern 514

---

Hi Mathecoach,

 

sollte man der Vollständigkeit halber in der 1. Teilaufgabe nicht auch das zweite mögliche Ergebnis angeben: f(x) = -2 * -4^x

?

 

Besten Gruß

Andreas

---

So wie du die Funktion notiert hast kannst du sie notieren. Dann kannst du aber das minus mal minus auch zu einem Plus zusammenfassen.

Aber eigentlich müsstest du wenn du bei

f(x) = k*a^x

die Werte einsetzt den Wert für a auch Klammern

Du erinnerst dich

x^2 ... wenn du für x = -1 einsetzt steht dort (-1)^2 und nicht -1^2

Wenn ich die -4 allerdings Klammer wie es nötig wäre habe ich ein Problem

f(x) = -2*(-4)^x

Weißt du welches Problem ich jetzt habe?

---

@Mathecoach:

Ich vermute, dass Du das "sprunghafte Verhalten" der Funktion meinst:

f(1) = -2 * (-4) = +8

f(2) = -2 * (-4)² = -2 * 16 = -32

f(3) = -2 * (-4)³ = -2 * (-64) = +128

Liege ich damit richtig?

---

Ja aber nicht nur das. Funktionen sind ja meist nicht nur für Ganzzahlige x definiert. Was ist denn wenn x = 0.5 ist ?

---

@Mathecoach:

You got me!

Das würde ja wohl bedeuten, dass man die Wurzel aus -4 ziehen müsste, ein Unding!!

Vielen Dank für Deine Korrektur!

---

Ich erinnere mich daran das mir auch mal in meiner Schulzeit dieser Fehler unterlaufen war.

Als ich dann den Graphen zeichnen wollte hab ich das aber irgendwie gemerkt, dass da was nicht stimmen kann.

---

Ja, das ist etwas tricky - schön, dass Du aufgepasst und mich auf meinen Fehler aufmerksam gemacht hast!

Danke nochmal!!

---

Es ist doch immer schön. Auch ich konnte heute schon von Lu etwas lernen :)

Man lernt nie aus.

---

Ein großes Wort gelassen ausgesprochen :-)