Man kann hier verschiedene Methoden der Begründung anwenden. (Auch Taylorreihen, aber davon schreibst du nichts)
Mal eine Antwort zu 1. Behauptung e^x > 1+x für x≠0
Betrachte die Graphen der beiden Funktionen.
f(x) = e^x und g(x) = x+1 mit f'(x) = e^x und g'(x) = 1
Zuerst zum Ausnahmefall x = 0
In x= 0 gilt f(0) =e^0 = 1 und g(0) = 1+0 = 0
Zudem in x = 0: f '(0) = e^0 = 1 und g'(0) = 1
Also: Die beiden Graphen berühren sich in (0,1).
Sei nun x > 0
f '(x) = e^x > 1 Die Kurve ist immer steiler als die Gerade. Die beiden Graphen können sich nicht mehr aneinander annähern.
Sei nun x < 0
f '(x) = e^x < 1 Die Kurve ist immer flacher als die Gerade. Die beiden Graphen können sich nicht mehr aneinander annähern.
Fazit: Kurve verläuft ausser in (0,1) oberhalb der Geraden. Also f(x) > g(x) qed.
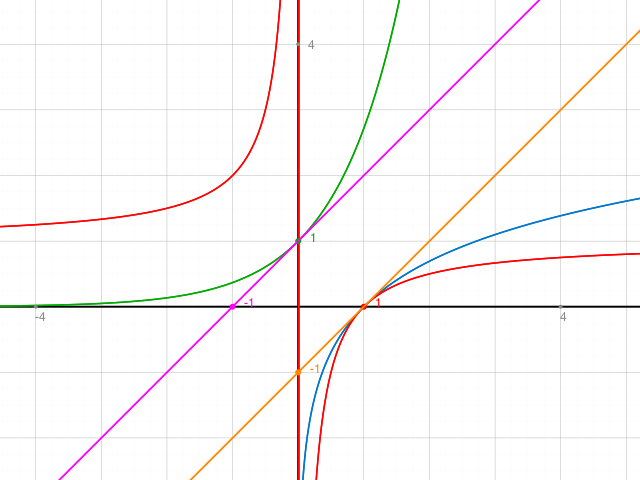
Illustration: violett und grün: Erste Ungleichung. rot und blau: Zweite Ungleichung.
Die 2. Ungleichung lässt sich wohl ähnlich wie die erste beweisen. Eventuell ist es einfacher, wenn du die Graphen an y=x spiegelst und die Umkehrfunktionen betrachtest.