Rekonstruktion einer Funktion 3. Grades mit Nullstelle (-1|0), Wendepunkt (-2|2), Punkt1 (0|4)

Question

Gesucht ist eine Funktionsgleichung 3. Grades.

Die Punkte habe ich schon, allerdings bekomme ich das Gleichungssystem nicht aufgestellt.

1. Nullstelle (-1|0)

2. Wendepunkt (-2|2)

3. Punkt1 (0|4)

4. Punkt2 (-1|0)

Wie lautet nun das Gleichungssystem?

Habe schon mehrere Ansätze, allerdings stimmt irgendwie keiner von denen

Comments

1. Nullstelle (-1|0)
4. Punkt2 (-1|0)

Hm...

---

Laut meinem Mathelehrer sollen wir diese Werte nehmen.

---

Aber wie Du selbst sehen kannst, unterscheiden sich die Bedingungen 1. und 4. doch ausschließlich durch ihren Namen...

---

Ja aber er meinte, dass das ein Extrema seie und man es in die 1. Ableitung einsetzen könne.

---

Wie lautet die Fragestellung ganz genau? So ist das nicht eindeutig lösbar.

EDIT: Zufällig klappt's doch. Da 4. nichts Zusätzliches fordert.

---

doch.

....................

---

1. Nullpunkt (-1|0)
2. Wendepunkt (-2|2)
3. Punkt P₁(0|4)
4. Extrempunkt P₂(-1|0)

1. f(-1) = 0
2. f(-2) = 2
2. f''(-2) = 0
3. f(0) = 4
4. f'(-1) = 0

Das sind dann insgesamt fünf Bedingungen,
vier wären angemessen...
 

Answer 1

Hi,

f(-1)=0   (Nullstelle bzw. Punkt2, diese sind identisch)

f(-2)=2   (Wendepunkt)

f''(-2)=0  (dessen Bedingung)

f(0)=4     (Punkt1)


Damit ergibt sich das Gleichungssystem:

-a + b - c + d = 0

-8a + 4b - 2c + d = 2

-12a + 2b = 0

d = 4


Löse und Du erhältst:

f(x) = x^3 + 6x^2 + 9x + 4


Grüße

Comments

Der Punkt ( -1 | 0 ) wäre dann auch ein Extrempunkt.
mfg Georg

---

Und was willste damit jetzt sagen?

Ist irrelevant da nicht vorgegeben (und nicht benötigt) und nicht erfragt ;).

Oder nur als zusätzliche Information? Q(-3|4) wäre ein Maximum?! :P

---

Auf diese Lösung sind wir auch heute im Unterricht gekommen.

Answer 2

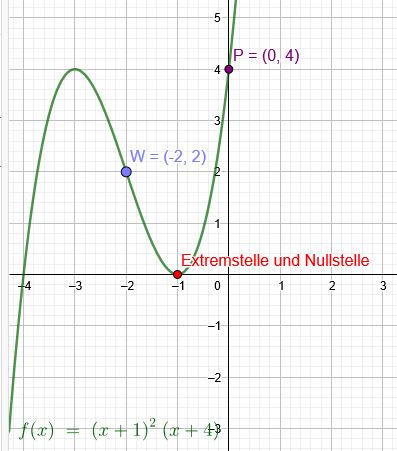
1. Nullstelle bei \(x=-1\)   ist auch eine Extremstelle somit eine doppelte Nullstelle
2. Wendepunkt \(W(-2|2)\)
3. \(P (0|4)\)

\(f(x)=a \cdot (x+1)^2\cdot(x-N)\)

\(P (0|4)\):

\(f(0)=a \cdot (0+1)^2\cdot(0-N)=-a \cdot N=4\)   →  \(a=-\frac{4}{N}\)

\(W(-2|2)\)

\(f(x)=-\frac{4}{N} \cdot (x+1)^2\cdot(x-N)\)

\(f(-2)=-\frac{4}{N} \cdot (-2+1)^2\cdot(-2-N)=-\frac{4}{N} \cdot(-2-N)=\frac{4}{N} \cdot(2+N)\)

\(\frac{4}{N} \cdot(2+N)=2\)  →\(N=-4\)        \(a=-\frac{4}{-4}=1\)

\(f(x)= (x+1)^2\cdot(x+4)\)

Comments

Zum fast Zehnjährigen?? :)

---

Genau. Ich hänge irgendwie an der Nullstellenform einer Parabel.