Kreis: Wie ist der Radius von x²-4x+y²+10y-18=0

Question

Wie berechne ich den Radius des Kreises. Kreisgleichung ist x²-4x+y²+10y-18=0

?

Answer 1

In der Funktiongleichung verstecken sich  zwei Binome, dahin umformen:

x²-4x+y²+10y-18

(x²-2x+4)-4 +(y"+10y+25)-25 -18=0

(x-2)²+(y+5)² -47 =0  |+47

(x-2)²+(y+5)²=47

daraus kann man nun den Radius und den Mittelpunkt bestimmen denn r²=(x-a)²+(y-b)²

r=√47  ≅6,85

und M = (2|-5)

Answer 2

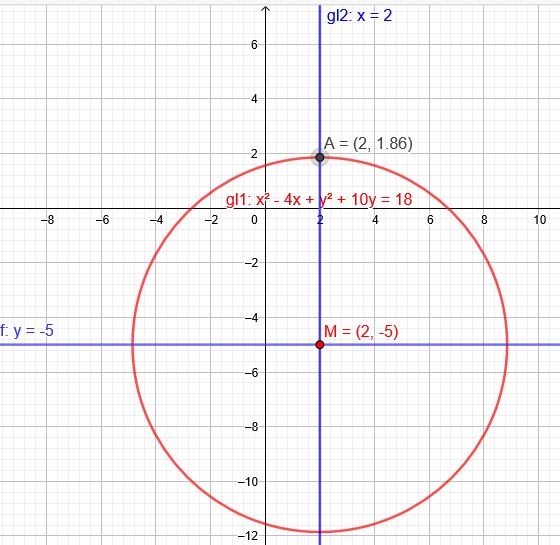
\(f(x,y)=x²-4x+y²+10y-18\)

\(\frac{df(x,y)}{dx}=2x-4\)

\(\frac{df(x,y)}{dy}=2y+10\)

\(2x-4=0\)→\(x=2\)

\(\frac{df(x,y)}{dy}=2y+10\)

\(2y+10=0\)→\(y=-5\)

Koordinaten des Kreismittelpunktes sind \(M(2|-5)\)

Schnitt \(x=2\) mit \(x²-4x+y²+10y=18\)       \(4-8+y²+10y=18\)        \(y²+10y=22  \)

\(y_1=-5- \sqrt{47} \)

\(y_2= \sqrt{47}-5 \)

Schnittpunkt mit Kreis   \(A(2|1,86\)    \(r=1,86+|-5|=6,86\)

\(f(2,-5)=4-8+25-50-18=-47\)

\( \sqrt{|-47|}=6,86 \) Das ist nun auch der Radius.

Comments

Die immer weiter um sich greifende Wahnvorstellung, primitive Algebra mit Methoden der höheren Analysis lösen zu müssen, ist wirklich bemerkenswert (euphemistisch gesprochen).