Kreise und Geraden - Radius eines Kreises

Question

Aufgabe:

Übung 3

Wie muss der Radius \( r \) des Kreises \( \mathrm{k} \) um den Mittelpunkt \( \mathbf{M}(3 \mid 2) \) gewählt werden, damit die Gerade \( g \) durch die Punkte \( \mathrm{A}(4 \mid 9) \) und \( \mathrm{B}(10 \mid 1) \)
a) eine Passante,
b) eine Tangente,
c) eine Sekante ist.

Problem/Ansatz:

Bitte um Lösung mit Lösungsschritten. Ich weiß leider nicht, wie hier vorzugehen ist.

Comments

eigentlich hätte es gereicht, sich eine Zeichnung zu machen ...

Durch Verschieben des roten Punktes kannst Du den Radius ändern.

---

siehe dazu auch https://www.mathelounge.de/989782/

Answer 1

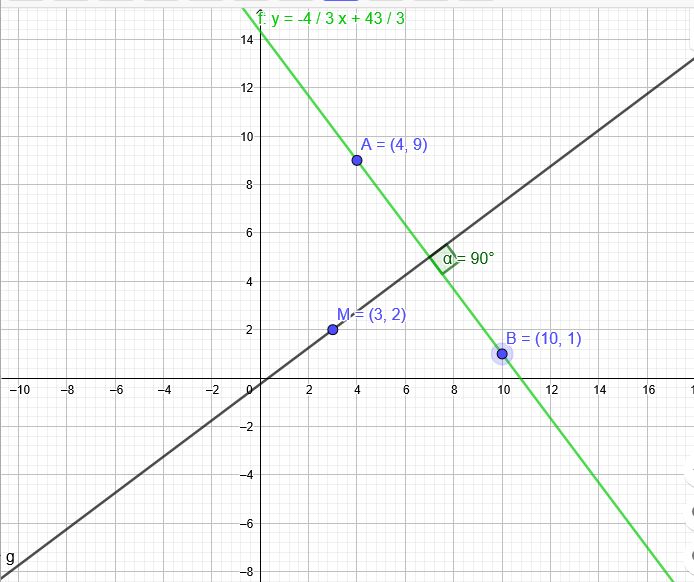
Wie muss der Radius \( r \) des Kreises \( \mathrm{k} \) um den Mittelpunkt \( \mathbf{M}(3 \mid 2) \) gewählt werden, damit die Gerade \( g \) durch die Punkte \( \mathrm{A}(4 \mid 9) \) und \( \mathrm{B}(10 \mid 1) \)

Berechnung der Geraden:

Allgemein:\(  \frac{y-y₁}{x-x₁}=\frac{y₂-y₁}{x₂-x₁} \)

\(  \frac{y-9}{x-4}=\frac{1-9}{10-4}=-\frac{4}{3} \)

\(  y=-\frac{4}{3}*(x-4) +9=-\frac{4}{3}*x+\frac{16}{3}+9=-\frac{4}{3}*x+\frac{43}{3}\)

Damit der Kreis die Gerade nirgends schneidet oder berührt, muss der Radius des Kreises kleiner sein als der Abstand von M zur Geraden.

Berechne zuerst den Abstand .

Hilfestellung ist in der Zeichnung gegeben:

Comments

Wie kommt man auf folgende Rechnung:

\(  y=-\frac{4}{3}*(x-4) +9=-\frac{4}{3}*x+\frac{16}{3}+9=-\frac{4}{3}*x+\frac{43}{3}\)

Ich kenne die Kreisgleichung nur so, dass man dort die Koordinaten des Kreises einsetzt (x-m1)^2 + (y-m2)^2 = r^2

---

\(  y=-\frac{4}{3}*(x-4) +9=-\frac{4}{3}*x+\frac{16}{3}+9=-\frac{4}{3}*x+\frac{43}{3}\)

Das ist die Berechnung der Funktion der Geraden durch A und B

Berechne hierzu die Normale (in der Zeichnung ist es die schwarze Gerade)

Schneide nun beide Geraden und du hast den Berührpunkt eines Kreises um M.

Nun kannst du mit der  Kreisformel \((x-x_M)^2+(y-y_M )^2=r^2\) den Radius bestimmen

---

Vielen Dank, würdest du mir verraten wie du diese Berechnung aufgestellt bzw. umgestellt hast?

Ich kenne nur y = mx+b, jedoch zur Bestimmung von b erstmal und dass dabei y eben den Y-Wert eines Punktes hat, was ja oben nicht der Fall ist

---

Weg über:

\(y = m*x+b\)

\(A(4|9)\)

1.)\(9 = 4*m+b\)   

\(B(10|1)\)

\(1 = 10m+b\) →\(b=1-10m\)  in 1.) \(9 = 4*m+b\) einsetzen:

\(9 = 4*m+1-10m=-6m+1\)

\(-6m+1=9\)   \(m=-\frac{4}{3}\)       \(b=1-10*(-\frac{4}{3})=1+\frac{40}{3}=\frac{43}{3}\)

\(y = -\frac{4}{3}*x+\frac{43}{3}\)

---

Woran wird eine Normale eigentlich festgemacht? Also es könnte ja viele Geraden geben, die senkrecht zu g verlaufen

---

In deinem Falle geht die Normale durch den Mittelpunkt des Kreises \(M(3|2)\)

Die Steigung der Geraden durch A und B hat die Steigung \(m=-\frac{4}{3} \)

Die Normalensteigung ist hier \(m_N= \frac{3}{4}\)

Jetzt kannst du die Punkt-Steigungsformel der Geraden anwenden:

\( \frac{y-y₁}{x-x₁}=m_N \)

Answer 2

Stelle eine Gleichung für g auf.

Stelle eine Gleichung durch M mit Steigung senkrecht zu g auf.

Finde den Schnittpunkt der beiden Geraden.

Rechne den euklidischen Abstand zwischen M und Schnittpunkt aus.

Das ist der Radius, bei dem g eine Tangente, unter dem g eine Passante und über dem g eine Sekante ist.

Answer 3

Eine Skizze hilft!

Trage die Punkte A, B und M in ein Koordinatensystem ein. Verbinde die Punkte A und B und verlängere die Gerade g über A und B hinaus.

Ein Kreis um M kann die Gerade g a) nicht schneiden (Passante), b) berühren (Tangente) oder c) in zwei Punkten schneiden (Sekante).

Um diese Fälle unterscheiden zu können, brauchst Du das Lot von M auf die Gerade g.

a) bedeutet Radius kleiner Lot, b) bedeutet Radius gleich Lot und c) bedeutet Radius größer Lot.

Viel Erfolg!