Ich habe im Internet nach Beispielaufgaben mit Lösungen gesucht (zu Konvergenzkriterien) und diese hier gefunden:
Lösung 11: \( \quad \sum \limits_{n=1}^{\infty} \frac{n^{5}}{2^{n}}=\frac{1}{2}+\frac{32}{4}+\frac{243}{8}+\ldots \)
\( \lim \limits_{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_{n}}\right|=\lim \limits_{n \rightarrow \infty} \frac{(n+1)^{5}}{2^{n+1}} \cdot \frac{2^{n}}{n^{5}}=\lim \limits_{n \rightarrow \infty} \frac{1}{2} \cdot\left(1+\frac{1}{n}\right)^{5}=\frac{1}{2}<1 \)
Die Reihe konvergiert.
Ich verstehe leider den markierten Teil dieses Schrittes nicht ganz:
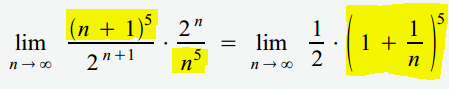
Mir ist klar, warum 2^n/(2^{n+1}) zu 1/2 wird aber nicht wie hier aus ((n+1)^5)/n^5 dann plötzlich (1+ (1/n))^5 wird, welche Art von Rechenregel wird da angewandt? Kann mir jemand das etwas feinschrittiger erklären?