Wahrscheinlichkeitsrechnung bei mehrstufigen Zufallsversuchen

Question

Hallo liebe Community!

Da wir gerade im Matheunterricht das Thema Wahrscheinlichkeitsrechnung behandeln und ich mir noch recht unsicher bei diesem Thema bin, habe ich mir mal eine Übungsaufgabe aus dem Internet geholt.

Natürlich ist da auch eine Lösung vorhanden, allerdings ist der Rechenweg nicht angezeigt und nun möchte ich von euch gerne wissen, ob ich mit meinem Weg richtig liege oder nur durch Zufall auf das gleiche Ergebnis stoße.

Folgende Aufgabe:

Es wird zweimal mit einem Würfel gewürfelt, wessen Netz unten angezeigt ist.

1). Berechne die Wahrscheinlichkeit, zwei gleiche Zahlen zu erwürfeln

2). Berechne die Wahrscheinlichkeit, erst eine größere und dann eine kleinere Zahl zu würfeln

3). Berechne die Wahrscheinlichkeit, zuerst eine 2 zu würfeln

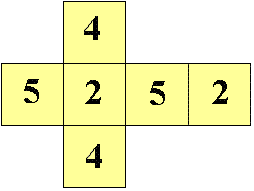
1). Zuerst habe ich mir natürlich den Würfel angesehen und habe mir gedacht, dass man nur 3 verschiedene Zahlen würfeln kann.

Nun habe ich als erstes alle möglichen Ergebnisse berechnet, die man durch zweimaliges Würfeln mit 3 verschiedenen Zahlen erreichen kann. Das wären doch 3² ?

Und nun hat man beim ersten Wurf 3 Möglichkeiten, da eine Zahl ja noch nicht festgelegt ist und somit die erste beliebig sein kann.

Beim zweiten Wurf hat man nur noch 1 Möglichkeit, da nur eine von den drei Möglichkeiten gleich sein kann.

Also: 3*1/3² = 3/9 = 1/3 = 33,33% ?

2). Beim ersten Wurf gibt es nur 2 Möglichkeiten, nachdem beim zweiten Wurf die Chance auf eine höhere Zahl besteht. Das wären die 4 und die 5. Nun gibt es bei der 4 aber nur eine Möglichkeit, beim zweiten Wurf eine kleinere Zahl zu erwürfeln. Bei der 5 gibt es 2 Möglichkeiten, also:

(2*1 + 2*2)/3²   aber bei der Lösung heißt es 1/3. Hier weiß ich jetzt nicht weiter

3). Das erklärt sich eigentlich von selbst. 1/3 :)

Und dann hätte ich noch eine Frage: Wie geht ihr bei solchen Aufgaben vor? Fragt Ihr euch zuerst ob es mehrstufig ist oder sowas? Manchmal bin ich mir bei solchen Aufgaben ziemlich unsicher...

Vielen Dank schonmal!

Answer 1

1). Deine Argumentation inkl. Resultat ist

Richtig.

2). Beim ersten Wurf gibt es nur 2 Möglichkeiten, nachdem beim zweiten Wurf die Chance auf eine höhere Zahl besteht. Das wären die 4 und die 5. Nun gibt es bei der 4 aber nur eine Möglichkeit, beim zweiten Wurf eine kleinere Zahl zu erwürfeln. Bei der 5 gibt es 2 Möglichkeiten, also:

(2*1 + 2*2)/3²   aber bei der Lösung heißt es 1/3. Hier weiß ich jetzt nicht weiter

5,4

5,2

4,2

sind aber nur 3 günstige Ausfälle. 1 + 2. Die roten 2en in deiner Argumentation stimmen nicht.

3). Das erklärt sich eigentlich von selbst. 1/3 :)

Und dann hätte ich noch eine Frage: Wie geht ihr bei solchen Aufgaben vor? Fragt Ihr euch zuerst ob es mehrstufig ist oder sowas? Manchmal bin ich mir bei solchen Aufgaben ziemlich unsicher...

Wenn man nicht sicher ist, einfach systematisch alle günstigen und möglichen Ausfälle aufzählen. Da erkennt man an der Grüppchen, die sich ergeben schnell, wie man das direkter haben könnte.

Answer 2

Zu 1)   Zweimal die gleiche Zahl (5) ----->  1/3 * 1/3 = 1/9 = 0,11 , also 11% !

Comments

Ok, auf welche Frage würde denn meine Antwort zutreffen?

Verstehe das mit den 11% ehrlich gesagt nicht. Würde das nicht auf eine am Anfang festgelegte bedingte Zahl zutreffen? Wie wenn ich sagen würde, wie hoch ist die Wahrscheinlichkeit 2 Einsen hintereinander zu würfeln?

Trotzdem :)

Answer 3

1). Berechne die Wahrscheinlichkeit, zwei gleiche Zahlen zu erwürfeln

P(22, 44, 55) = 2/6 * 2/6 * 3 = 1/3 = 33.33%

2). Berechne die Wahrscheinlichkeit, erst eine größere und dann eine kleinere Zahl zu würfeln

P(42, 54, 52) = 2/6 * 2/6 * 3 = 1/3 = 33.33%

3). Berechne die Wahrscheinlichkeit, zuerst eine 2 zu würfeln 

P(2x) = 2/6 = 1/3 = 33.33%

Comments

Wie geht ihr bei solchen Aufgaben vor? Fragt Ihr euch zuerst ob es mehrstufig ist oder sowas? Manchmal bin ich mir bei solchen Aufgaben ziemlich unsicher...

Ja. Die erste Frage ist ob es mehrstufig ist. Dann ist die Frage wie die Menge an Ereignissen aussieht, zu denen die gefragte Wahrscheinlichkeit passt. Als letztes berechne ich dann die Wahrscheinlichkeit für meine Menge. Dabei kann ich dann die Pfadregeln benutzen.