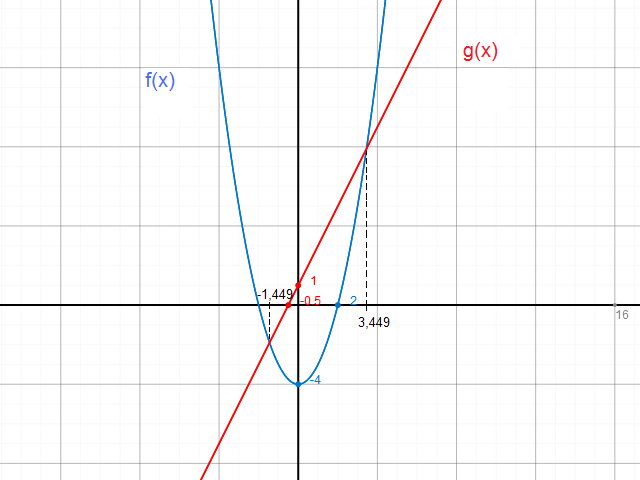
man nehme am besten 2 funktionen als beispiel, hier f(x) und g(x)
$$f(x)=x^2-4$$
$$g(x)=2x+1$$
$$f(x)=g(x)$$
$$x^2-4=2x+1 |-2x ; -1$$
$$x^2-2x-5=0 | pq formel$$
$$x^2+px-q=0$$
$$x_{1,2}=-(\frac{p}{2}) \pm \sqrt{(\frac{p}{2})^2-q} $$
$$x_{1,2}=-(\frac{-2}{2}) \pm \sqrt{(\frac{-2}{2})^2+5} $$
$$x_{1,2}=1 \pm \sqrt{6} $$
$$x_1=3,449$$
$$x_2=-1,449$$
die Lösungen dieser Gleichung (nullstellen) sind die Schnittpunkte der Graphen, dies kann man noch überprüfen indem man den wert in die Gleichungen einsetzt und es wird ein gleicher Funktionswert raus kommen.
hier:
$$f(3,449)=(3,449)^2-4=7,89$$
$$g(3,449)=2*(3,449)+1=7,89$$
$$f(-1,449)=(-1,449)^2-4=-1,9$$
$$g(-1,449)=2*(-1,449)+1=-1,9$$
wobei man hier beachten muss, dass ich gerundet habe, normalerweise musst du immer genau mit dem gleichen Ergebnis weiter rechnen, auch wenn es sehr viele Nachkommastellen sind, da kannst du ja einfach an deinem Taschenrechner die taste Ans (so heißt sie bei meinem) nutzen damit du das Ergebnis der letzten Berechnung verwenden kannst.
habe dir noch ein kleines bild beigefügt woran man es auch noch anhand der beiden Graphen sehen kann ;)
mfg, Subis