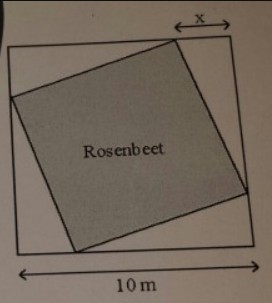
Die Rosen reichen für ein quadratisches Beet von \( 70 \mathrm{~m}^{2} \) Fläche. Berechne das zugehōrige \( x \).
Bei diesem \( x \) ist die Fläche des quadratischen Rosenbeets größer als die des rechteckigen Rosenbeets bei dem gleichen \( x \).
Weise nach, dass für alle \( x \) die Fläche des quadratischen Rosenbeets größer oder gleich der Fläche des rechteckigen Rosenbeets bei dem gleichen \( x \) ist.
Ansatz:
Ist das so richtig berechnet?
1.c²=a²+b²
2. 70=x²+(10-x)²
3. 70=x²+100-20x+x²
4. 0=2x²—20x+(100-70); x^1=8,16; x²=1,84