Funktionen f und g mit f(x) =2*x^2 +4x-1.....

Question

Bitte helft mir , ich kanns noch nicht!!

Gegeben seien die beiden Funktionen  f und g     mit    f (x) = 2 * x² + 4x  - 1 und

g(x) = 0,5 * x + 6,5

a) Bestimmen Sie den Scheitelpunkt und die Nullstellen der Funktion f.

b) Durch welche geometrische Operationen können Sie den graphen der Funktion f aus der Normalparabel erhalten ?

c) Stellen Sie f  graphisch da.

d) Stellen Sie im gleichen Koordinatensystem von Teilaufgabe c) den graphen von g dar

e) Lösen Sie das Gleichungssystem :

y= 2 x ²+ 4x -1

y= 0,5 +6,5  graphisch. Begründen Sie ihre n Lösungsweg.

f) Lösen sie das Gleichungssystem aus Teilaufgabe e) rechnerisch.

g) Welches Monotonieverfahren zeigen die Funktionen f und g ?

Lieben Gruß Pia

Comments

a)allgemeine Lösungsformel Parabel und Scheitelpunktform googeln

b) Streckung/Stauchung

c +d) Onlinefunktionsplotter

e) Gleichsetzungsverfahren (googeln)

---

@Pia: Ich würde das zwar versuchen, aber das würde schon bisschen dauern^^

---

lass dir Zeit, es ist lieb, dass du mir helfen möchtest, ich habe echt bammel...ob ich es jemals kann...

gruß Pia

---

Hallo Pia,

Tut mir echt leid. Ich musste noch mein Koffer packen. Ich mach mich jetzt sofort ran :)

Answer 1

Hi nochmal Pia^^

So Du has 2 Funktionen gegeben. Eine Quadratische und eine Lineare Funktion;

f(x) = 2x²+4x-1 und  g(x) = 0,5x+6,5

a)

Nullstellen:

Du musst erstmal diese Gleichung in die Normalform bringen, um dann die pq-Formel anzuwenden (narürlich kanns Du auch die abc/Mitternachtsofmel benutzen^^)

Um die pq-Formel zu benutzen musst Du die 2 vor dem x² weg bekommen und das kriegs Du weg indem Du geilt durch 2 rechnest, also:

2x²+4x-1=0 |:2

x²+2x-0,5=0 |pq-Formel

x₁=(-2+√6)/2

x₂=(-2-√6)/2

Scheitelpunktform:

2x²+4x-1

2(x²+2x-0,5)

2(x²+2x+1-1)-0,5

2(x+1)²-2-1

2(x+1)²-3

S(-1|-3)

b)

schaffst Du alleine?

c) + d)

Solltest Du auch eigentlich alleine schaffen? Erstelle Dir eine Wertetabelle (kannst es auch mit dem TR erstellen) und dann trägst Du die Punkte in dein Koordinatensystem ein. Bei der Linearen Funktion kannst Du es auch ohne Wertetabelle zeichen. Unzwar so:

Du kennst die allgemeine Form der linearen Funktion: y=mx+b, wobei m die Steigung und b der y-Achsenabschnitt ist.

g(x)= 0,5x+6,5

Du weißt, dass 0,5 die Steigung ist und 6,5 der y-Achsenabschnitt.

1.Schritt: Du gehst auf die y-Achse und trägst bei 6,5 einen kleinen Kreuz (das ist dein erster Punk).

2. Du gehst von dem Punkt 1 Einheit nach Rechts und ann +0,5 nach oben.

3. Fertig :)

So sollte es dann aussehen:

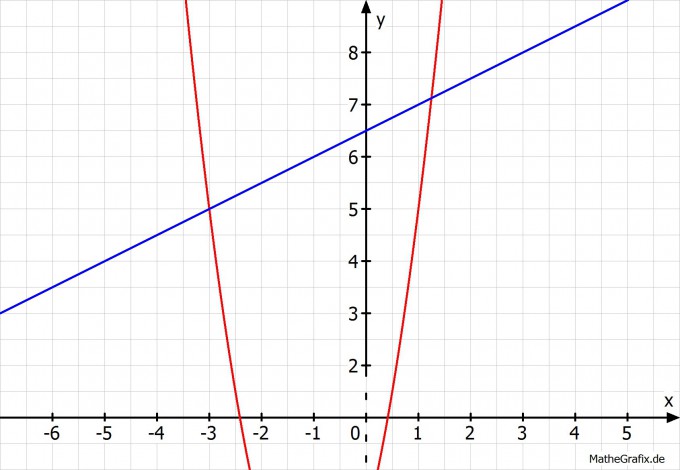
e)

Also zeichnerisch lösen ist etwas ungenau hier, aber wir können es mal versuchen^^

Die Lösungen sind einfach die Schnitpunkte. Die kannst Du ablesen:

x₁= -3

y₁= 5

x₂≈ 1,3

y₂≈ 7,1

f)

Jetzt lösen wir das mal rechnerisch. Dies machen wir indem wir diese beiden Gleichungen gleichsetzen, also:

2x²+4x-1=0,5x+6,5 |-0,5x

2x²+3,5x-1= 6,5 |-6,5

2x²+3,5x-7,5=0 |:2

x²+1,75x-3,75=0 |pq-Formel

x₁= -3

x₂= 1,25

Du siehst wir waren zeichnerisch ziemlich knapp^^

Nun kannst Du auch die x-Werte in die Gleichung einsetzen um die y-Werte auszurechnen :-)

g)

Also hier will ich Dir jetzt nichts falsches beibringen. Da ich noch keine Kurvendiskussion oder ähnliches hatte^^ Ich bin erst seit 2 Tagen in der 11.Klasse^^

Ich hoffe dass ich Dir trotzdem irgendwie bisschen geholfen habe? :)

Grüße

Comments

...........danke dir, ich seh mal wie ich morgen damit klar komme, jetzt bin ich zu müde....

Alles Gute für deine Reise !!!!!

gruß Pia

---

Kein Problem. Hoffe da ist soweit alles richtig. Ich denek aber schon, denn sonst hätte der Mathecoach kommeniert :D

Gute Nacht und Danke^^

---

Genau Emre. Das sieht tatsächlich alles sehr gut aus. Mein Glückwunsch. Ich hatte es zur Kontrolle auch nochmal gerechnet und komme auf die gleichen Sachen. Ich habe auch noch g gemacht. Hier wird nur gefragt in welchem Intervall die Funktionen steigen oder fallen.

---

Jaaaaaaaaaaaaaa so eine Nachricht vom Mathecoach zu hören freut mich immmmmmmmer :)

---

...........ihr seid ja süß ihr zwei, soviel loyalität ,toll, ich freu mich auf ein nächstes Mal

---

Ich auch bis zum nächsten mal :)

Und nun Gute Nacht an euch beide. Muss Morgen früh aufstehen^^

---

.....nadann ab ins Körbchen, hoffentlich hilft man dir die Tage auch,-gute Nacht Emre

Answer 2

Gegeben seien die beiden Funktionen f und g mit

f(x) = 2·x^2 + 4·x - 1 und g(x) = 0.5·x + 6.5

a) Bestimmen Sie den Scheitelpunkt und die Nullstellen der Funktion f.

f(x) = 0

2·x^2 + 4·x - 1 = 0   | abc-Formel

x = -1 ± √6/2

x = -2.225 ∨ x = 0.225

Sx = -1   [Das ist das was vor ± √6/2 steht]

Sy = f(-1) = -3

Scheitelpunkt S(-1 | -3)

b) Durch welche geometrische Operationen können Sie den Graphen der Funktion f aus der Normalparabel erhalten?

Strecken in Y-Achsenrichtung mit dem Faktor 2. Verschieben um 1 Einheit nach links und 3 Einheiten nach unten.

c) Stellen Sie f  graphisch da.

d) Stellen Sie im gleichen Koordinatensystem von Teilaufgabe c) den Graphen von g dar.

e) Lösen Sie das Gleichungssystem

y = 2·x^2 + 4·x - 1

y = 0.5·x + 6.5

graphisch. Begründen Sie ihren Lösungsweg.

Hier brauche ich nur die Schnittpunkte in etwa ablesen.

ca. bei x = -3 ∧ y = 5

ca. bei x = 1.3 ∧ y = 7.1

f) Lösen sie das Gleichungssystem aus Teilaufgabe e) rechnerisch.

2·x^2 + 4·x - 1 = 0.5·x + 6.5

2·x^2 + 3.5·x - 7.5 = 0   | abc-Formel

x = 1.25 ∨ x = -3

g(1.25) = 7.125

g(-3) = 5

g) Welches Monotonieverfahren zeigen die Funktionen f und g?

f ist für x ≤ -1 streng monoton fallend und für x ≥ -1 streng monoton steigend.

g ist streng monoton steigend.

Comments

Hr. Mathecouch, ich danke Ihnen für die hilfreichen Ergänzungen...

Einen schönen und erholsamen Abend noch.

Gruß Pia

Answer 3

das ist ja auch Wichtig, ich freu mich, das du mich nicht vergessen hast.

Machst dich wohl morgen auf große Fahrt ??

Lieben gruß Pia

Comments

Hi Pia,

also ich mache eine Stottertherapie und ich muss nach Kassel. Ich muss da bis Samstag übernachten^^

also paar Tage^^