Extremwertaufgabe: maximales Volumen Kegel

Question

Aufgabe Brunnen:

Ein Steinmetz soll nach folgendem Plan einen kunstvollen Brunnen bauen:

1. Von einer steinernen Halbkugel mit dem Radius \( \mathrm{R}=3 \mathrm{~m} \) aus dem historischen Besitz der Stadt soll die obere Kappe horizontal abgetrennt werden. Die Schnittfläche ist ein Kreis mit dem Radius \( \mathrm{r} \).

2. Von der Schnittfläche ausgehend soll eine kegelförmige Öffnung in den Stein getrieben werden, deren Spitze bis zur Bodenmitte der Halbkugel reicht.

Ermitteln Sie das maximale Fassungsvermögen des Brunnens.

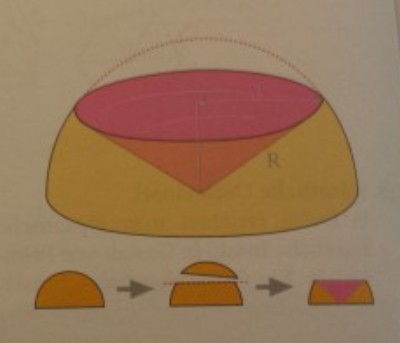
Ansatz:

Also soweit ich das verstanden habe, soll ich ein maximales Volumen für den violetten Bereich finde (also für den Kegel), liege ich da richtig? Dafür habe ich dann das Volumen errechnet, jedoch bekomme ich nur ein Minimum heraus. Da muss ich doch was falsch gemacht haben!

Hab als Hauptbedingung Volumen des Kegels und als NB: r²=h²-9.

Könnte mir bitte jemand seinen Rechenweg schildern?

Answer 1

V = 1/3 * G * h = 1/3 * pi * r^2 * h = 1/3 * pi * √(3^2 - h^2)^2 * h = 3·pi·h - pi·h^3/3

V' = 3·pi - pi·h^2 = 0
h = √3

V = 3·pi·(√3) - pi·(√3)^3/3 = 2·√3·pi = 10.88 m^3