Aufgabe Sinusfunktion:
Jede reelle Zahl x kann als Bogenmaß eines Winkels aufgefasst werden. Daher ist für jedes x ∈ ℝ gemäß der nachstehenden Abbildung die Zahl sin(x) definiert.
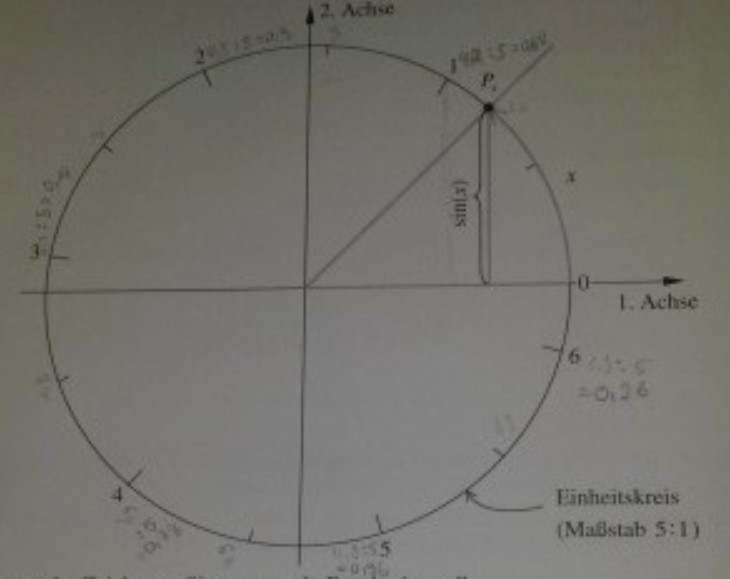
a) Lies aus der Zeichnung Sinuswerte ab. Runde sinnvoll.
b) Überprüfe die Ergebnisse in a) mit dem Taschenrechner.
c) Besondere Sinuswerte: Fülle die Tabelle aus und präge sie dir ein.
| x | 0 | π/6 | π/4
| π/3
| π/2
| (2/3)·π | (3/4)·π | (5/6)·π | π
| (3/2)·π | 2π |
| sin(x) |
|
|
|
|
|
|
|
|
|
|
|
Aus Klasse 9: sin(30°) = 1/2; sin(45°) = (1/2)·√2; sin(60°) = (1/2)·√3
d) Veranschauliche in der Abbildung die Zahl sin(-x) und vergleiche mit sin(x).
e) Was lässt sich über sin(x + 2π) sagen?