Trigonometrische Funktion Periode

Question

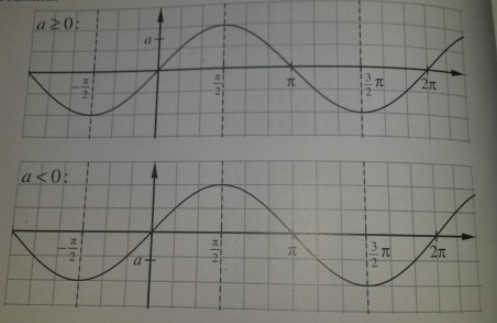
a) Erläutere an den Abbildungen folgenden Sachverhalt:

„Die Gleichung \( \sin (x)=a \) mit \( -1 \leq a \leq 1 \) hat in \( \left[-\frac{\pi}{2}: \frac{x}{2}\right] \) genau eine Lösung.“

A: "Die in \( \left[-\frac{\pi}{2} ; \frac{\pi}{2}\right] \) liegende Lösung von \( \sin (x)=a \) wird mit arcsin(a) (lies: Arcussinus von a) bezeichnet.

B: Der Taschenrechner liefert diese Lösung ( \( \sin ^{-1} \)-Taste im RAD-Modus).

Markiere die Lösung arcsin(a) in der Abbildung.

b) Löse folgende Gleichungen in \( \left[-\frac{\pi}{2} ; \frac{\pi}{2}\right] \) und gib die Lösungen auf zwei Dezimalen gerundet an.

sin(x) = 0,435 x=arcsin(0,435) ≈ 0,45	sin(z) = -0,581
sin(x) = 0,8415	sin(u) = -0,9998
sin(x) = 0,98	\( \sin (x)=-\frac{1}{3} \sqrt{2} \)

Answer 1

mit -1 ≤ a ≤ 1 ist der "y-Wert" der Sinusfunktion gemeint. Wenn man sich das in den Schaubildern anschaut und Parallelen zur x-Achse durchlegt, die den Wert a haben, also y = a, dann sieht man, dass der Sinus immer nur einmal geschnitten wird. Es gibt also auch nur eine Lösung innerhalb des gegebenen Intervalls.

Grüße