Also da gibt es mehrere Möglichkeiten. Ich habe das jetzt so gelöst: Ich habe die gesamte Fläche des Quadrats in einzelne Flächen, die von x abhängen, aufgeteilt:
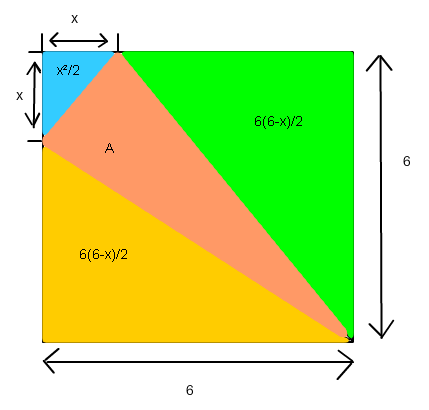
Die Summe aller einzelnen Flächeninhalte ergibt das gesamte Quadrat. Dann habe ich eine Funktion aufgestellt, in der der Flächeninhalt A des Dreiecks von x abhängt:
\( \frac{x^{2}}{2}+\frac{6(6-x)}{2}+\frac{6(6-x)}{2}+A=6^{2} \)
\( \frac{x^{2}}{2}+36-6 x+A=36 \)
\( A(x)=-\frac{x^{2}}{2}+6 x \)
Das kann man nun ableiten und den Hochpunkt für ein x berechnen.
\( A(x)=-\frac{x^{2}}{2}+6 x \rightarrow \text{max.} \)
\( A^{\prime}(x)=-x+6 \)
\( A^{\prime}(x)=0 \)
\( -x+6=0 \)
\( x=6 \)
Wenn x=6 ist, ist der Flächeninhalt also maximal. Zeichnet man das ein:
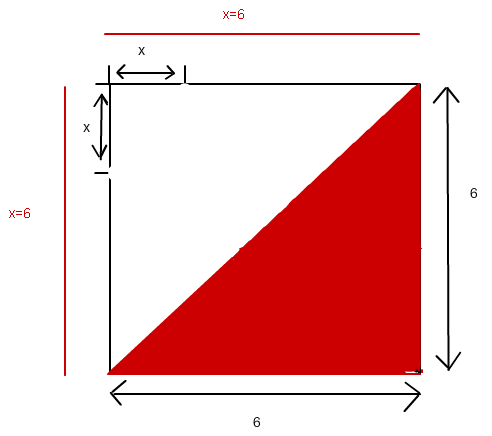
Da sieht man sofort, dass zwei Seiten 6 lang sind und die andere gemäß Satz des Pythagoras 6^2 + 6^2 = c^2 ↔ c= √72 = 8,49
Das Ergebnis kommt mir ein wenig komisch vor, ich weiss nicht, ob das so sein soll. Vielleicht könnte mich jemand bestätigen (oder widerlegen), ob das auch der Definition eines gleichschenkligen Dreieckes entspricht. Aber eigentlich doch schon, oder? 2 gleich lange Seiten...
Da fallen aber auch 3 Ecken mit Quadratecken zusammen, nicht nur eine... Also ich bin mir unsicher ;)