Ich habe einen Lückentext zum Thema Extrema bei Funktionenscharen.
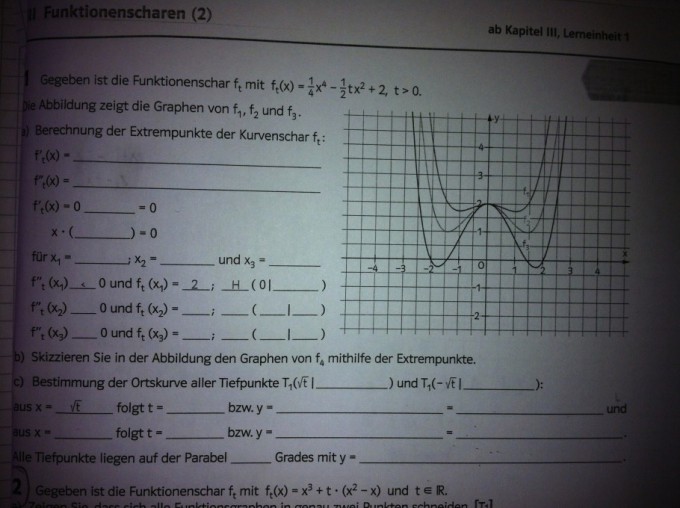
Gegeben ist die Funktionenschar \( f_{t} \) mit \( f_{t}(x)=\frac{1}{4} x^{4}-\frac{1}{2} t x^{2}+2, t>0 \)
Die Abbildung zeigt die Graphen von \( f_{1}, f_{2} \) und \( f_{3} \).
Berechnung der Extrempunkte der Kurvenschar \( \mathrm{f}_{\mathrm{t}} \):
Die Ableitungen sind ja leicht: f 't(x) = x3 - 1tx
f ''t(x) = 3x2 - 1t