Gleichung einer Ortslinie bestimmen:

Question

ich habe die Aufgabe, eine Ortskurve der Hochpunkte von f zu bestimmen. Für f_t gilt f_t(x)= x^{3} + tx^{2}.

Hochpunkt ist (-(2/3)t | (4/27)t^{3}).

Ich verstehe jetzt nicht, wie aus x = -(2/3)t und y = (4/27)t^{3}; t = (-3/2)x folgt (Abgesehen davon wird das nicht in meinem Buch erläutert).

, Florean :-)

Comments

Der Versuch f(x) = x gleichzusetzen ist auch gescheitert.

---

Bin etwas weiter: x = (-2/3)t somit ist t = (3/2)x

---

vermutlich ist \(t>0\) gemeint.$$\text{Aus }x=-\frac23t\text{ folgt }t=-\frac32x.$$$$\text{Aus }y=\frac4{27}t^3\text{ folgt }y=\frac4{27}\cdot\left(-\frac32x\right)^3=-\frac12x^3.$$

---

Endlich! Die Lösung:

Wir setzen Parameter t in den ermittelten y-Wert des Hochpunktes (4/27)t^{3} ein und erhalten somit y = (-1/2)x^{3}

Grüße

---

Genau, es gilt t > 0. Trotzdem Danke für deine Antwort :-)

Answer 1

f(x) = x^3 + t·x^2

Extrempunkte f'(x) = 0

3·x^2 + 2·t·x = 0 

Wir lösen das jetzt nach t auf

t = - 3/2·x

Damit bei x ein Extrempunkt ist müssen wir t = -3/2·x setzen. Das setzen wir also nun in die Funktion für t ein

f(x) = x^3 + t·x^2

f(x) = x^3 + (- 3/2·x)·x^2 = - x^3/2

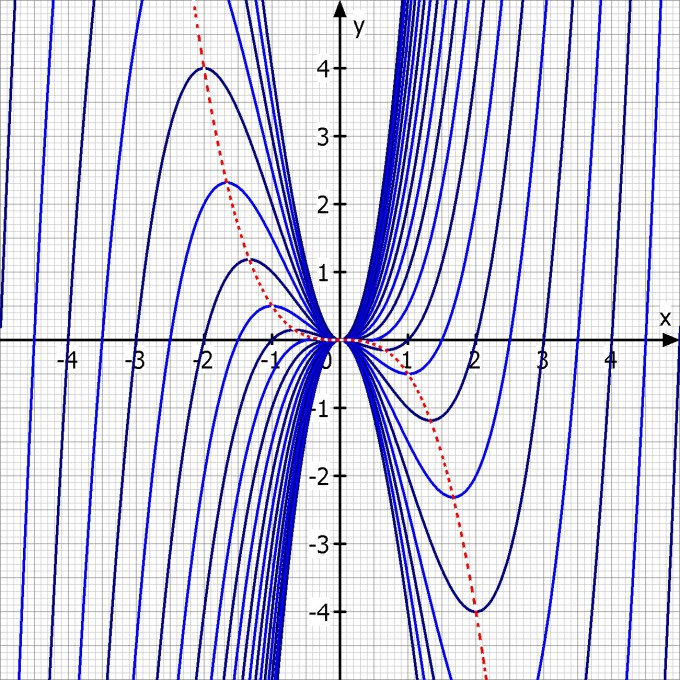
Das ist die Gleichung für die Ortskurve der Extrempunkte.

Für t > 0 haben wir an der Stelle Hochpunkte und für t < 0 haben wir an der Stelle Tiefpunkte.
Skizze: