Schon wieder ich! *.*
Doch dieses Mal verzweifelter!
Nummer b) ist die erklärbar?

Das Forto zeigt eine Hängebrücke. Die Stahlseile sind in einer Höhe von 80 m über der Sraße an den Brückenpfeilern befestigt. Der Verlauf des Stahlseils zwischen den Brückenpfeilern kann annähernd durch eine Parabel beschrieben werden.
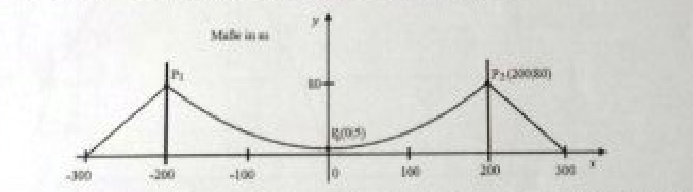
a) Eine der folgenden Funktionsgleichungen gehört zu der Parabel, den den Verlauf des Stahlseils beschreibt:
\((A) f(x)=-0,001875x^2+5\quad (B) f(x) = 0,001875x^2+5\quad (C) f(x)=0,001875x^2-5\)
Nenne diese und erkläre, warum die die beiden anderen Funktionsgleichungen die Parabel nciht beschreiben.
b) Die folgende Abbildung zeigt eine Hängebrücke. Die Stahlseile sind in einer Höhe von 48 m über der Straße an den Brückenpfeilern befestigt.
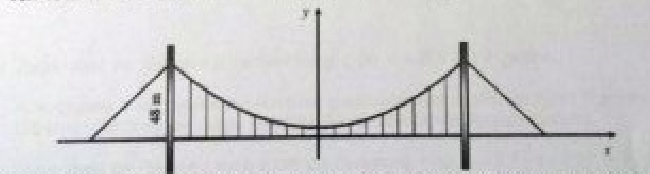
Das Stahlseil zwischen den Brückenpfeilern hat annähernd die Form einer Parabel mit der Funktionsgleichung \(f(x)=0,002x^2+3\) (x und f(x) in Metern).
Berechne mit Hilfe der Funktionsgleichung den Abstand zwischen den Brückenpfeilern.