Aufgabe 2:
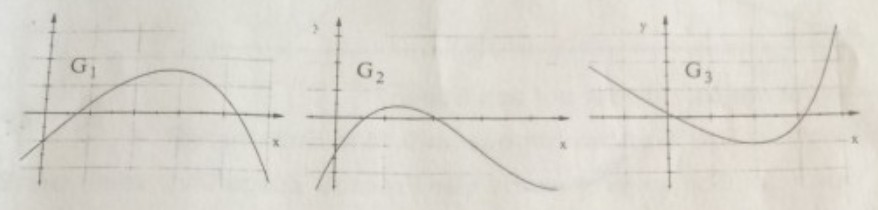
Die Funktion \( h \) mit \( h(x)=x-e^{\frac{1}{4}^{x}} \) hat das Schaubild \( K_{h} \). Zwei der gezeigten Schaubilder können nicht \( \mathrm{K}_{\mathrm{h}} \) sein.
Begründen Sie mit Hilfe jeweils einer Eigenschaft, welche Graphen nicht \( \mathrm{K}_{\mathrm{h}} \) sein können.
Aufgabe 3:
Gegeben ist \( K_{f} \) mit \( f(x)=3-e^{x} \)
a) Bestimmen Sie die Achsenschnittpunkte und Asymptote.
b) Geben Sie ohne zu berechnen an, wie sich die Nullstellen und Asymptoten verändern, wenn gilt:
1. \( f^{*}(x)=f(-x) \)
2. \( f^{* \star}(x)=-f(x) \)
3. \( f^{* * *}(x)=f(x-2) \)