Hallo GC,
f(x) = (x^2 - 2·x) · e^{0.5·x}
Mit der Produktregel erhältst du die Ableitungen:
f '(x) = 1/2 · e^{x/2} · (x^2 + 2·x - 4)
f "(x) = 1/4 · x · e^{x/2} · (x + 6)
Kurvendiskussion
Man betrachtet - bei "normal üblichen Funktionen" - vor allem folgende Punkte:
1) Definitionsbereich
Wenn dieser nicht angegeben ist, bestimmt man den maximal möglichen Definitionsbereich
In der Schule:
Dmax = ℝ \ { x ∈ ℝ | im Funktionsterm wird ein Nenner 0, der Radikand einer Wurzel negativ, das Argument eines Logarithmus ≤ 0 oder das Argument eines Tangensterms = π/2 + k·π (k∈ℤ) ... }
Bei dir ist D = ℝ
2) Symmetrie
Man prüft, ob die Funktion symmetrisch zum Ursprung oder zur zur y-Achse ist. Voraussetzung dafür ist natürlich ein symmetrischer Definitionsonsbereich ( wenn x eine Lücke ist, muss auch -x eine sein)
f(-x) = f(x) f.a. x ∈ D → Symmetrie zur y-Achse
f(-x) = - f(x) f.a. x ∈ D → Symmetrie zum Ursprung
Bei dir liegt keine dieser Symmetrien vor, weil der e-Term z.B für x = ± 1 völlig verschieden Beträge hat.
3) Nullstellen (Vorzeichenverlauf von f)
Gleichung f(x) = 0 lösen [ e-Term > 0 ]
(x^2 - 2·x) · e^{0.5·x} = 0 ⇔ x · (x - 2) · e^{0.5·x} = 0
⇔ x = 0 oder x = 2
4) Verhalten an den den Randstellen des Definitionsbereichs
limx→+∞ f(x) = ∞ ; limx→ -∞ f(x) = 0
weil der e-Term den Einfluss des Polynoms überwiegt.
5) Extremwerte und Monotonie
f '(x) = 0 ergibt die möglichen Extremstellen xE
f "(xE) > 0 → T , f "(xE) < 0 → H
bei f "(xE) = 0 prüft, ob und wie f ' bei xE das Vorzeichen wechselt.
wenn VZW + → - hat man einen Hochpunkt
wenn VZW - → + hat man einen Tiefpunkt
wenn kein VZW vorliegt, hat man einen Sattelpunkt
Den VZW von f " kann man auch immer statt des Einsetzens in f " als Eintscheidunggskriterium für H|T|S nehmen.
Die Monotonieintervalle erhält man durch die Bedingungen f '(x) ≥ 0 und f "(x) ≤ 0
1/2 · e^{x/2} · (x^2 + 2·x - 4) = 0 ⇔ (x^2 + 2·x - 4) = 0
pq-Formel → x = -1 ± √5 → x1 ≈ 1,24 ; x2 ≈ - 3,24
f "( 1,24 ) > 0 → T( 1,24 | -1,75 )
f "( -3,24 ) < 0 → H( - 3,24 | 3,34 )
6) Wendepunkte und Krümmung
f " (x) = 0 ergibt die möglichen Wendestellen xw
f '''(xE) ≠ 0 → W , bei f '''(xE) = 0 prüft man den VZW von f " an der Stelle xW prüfen.
Die Krümmungsintervalle erhält man aus den Bedingungen
f "(x) >0 → Links- , f "(x) < 0 → Rechtskrümmung
1/4 · x · e^{x/2} · (x + 6) = 0 → x1 = 0 ; x2 = - 6 (jeweils mit VZW von f ")
→ W1 ( 0 | 0 ) ; W2 (- 6 | 2,39 )
[ 7) ggf. Verhalten an den Definitionslücken (Grenzwerte) entfällt
(z.B. Polstellen bei gebrochen rationalen Funktionen) ]
8) plausiblen Graph zeichnen
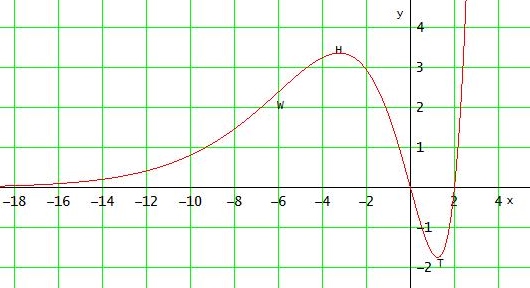
Gruß Wolfgang
