Betragsgleichungen lösen: |(x+2)^2| = 2 und |x| + |2-x| = 4

Question

Betragsgleichungen lösen:

1. |(x+2)^{2}| = 2

2. |x|+|z-x| = 4

Comments

Bei der ersten Gleichung kann man die Betragsstriche weglassen, da es sowieso quadriert wird.

Answer 1

Betragsgleichungen

1. |(x+2)^2| = 2

(x+2)^2 = 2

(x+2) = ±√2,
x_1,2 = -2 ± √2

2. |x| + |2-x| = 4
 
1. Fall x<0    
-x + (2-x) = 4
-2 = 2x    
-1 = x

2. Fall 0≤x≤2
x +(2-x) = 4
2 = 4
Keine Lösung zwischen 0 und 2.

3. Fall x> 2
x -(2-x) = 4
2x = 6
x = 3

Insgesamt L = { -1, 3}

Answer 2

Also erstens sind das keine Bruchgleichungen, weil ja nirgendwo ein Bruch auftaucht. Nun zu zweitens
Zu (a) \( |(x+2)^2|=(x+2)^2=x^2+4x+4=2 \) das kann man mit der pq-Formel lösen
Zu (b) Du musst hier Fallunterscheidungen machen und zwar \( x \ge 0\) oder \( x <0 \) und \( 2-x \ge 0 \) oder \( 2-x<0 \)
Damit hast Du vier zu untersuchende Fälle. Als Lösungen ergeben sich \( x=-1 \) und \( x=3 \)

Answer 3

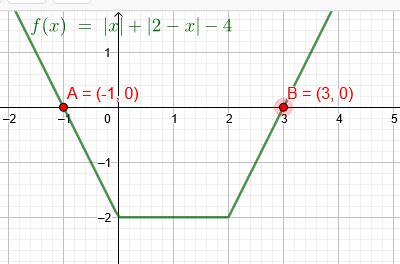
\(|x|+|2-x| = 4\)

\(\sqrt{x^2}+\sqrt{(2-x)^2} = 4   |\red{^{2}}\)

\(x^2+(2-x)^2+2\sqrt{x^2}\cdot \sqrt{(2-x)^2} = 16  \)

\(x^2+4-4x+x^2+2\sqrt{x^2(2-x)^2} = 16  \)

\(\sqrt{x^2(2-x)^2} = 6 -x^2+2x |\red{^{2}}\)

\(x^2(2-x)^2 = (6 -x^2+2x )^2\)

\((2x-x^2)^2 = (6 -x^2+2x )^2\)

\((2x-x^2)^2 - (6 -x^2+2x )^2=0\)  3.Binom:

\([(2x-x^2) +(6 -x^2+2x )][(2x-x^2) -(6 -x^2+2x )]=0\) Satz vom Nullprodukt:

1.)

\(2x-x^2 +3 =0\)

\(x_1=-1\)

\(x_2=3\)

Probe, da Quadrieren keine Äquivalenzumformung ist:

\(|-1|+|2+1| = 4\)✓

\( | 3 |+| 2-3 | = 4\)✓     

2.)

\(2x-x^2 -6 +x^2-2x )]=0\)

\(0=0\)