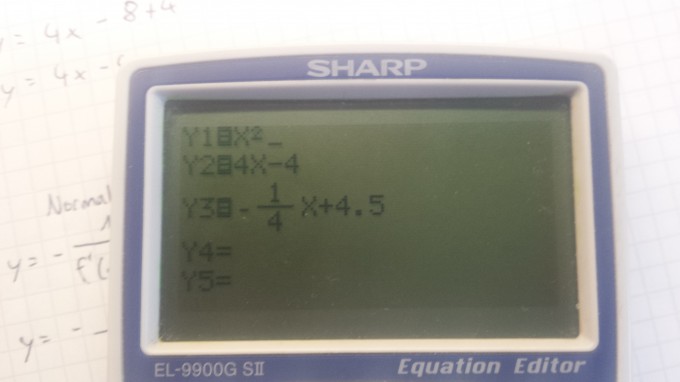Bestimmen Sie die Gleichungen der Tangente und der Normalen an den Graphen der Funktion \( \mathrm{f} \) an der Stelle \( \mathrm{u} \).
a) \( f(x)=x^{2} ; u=2 \)
b) \( f(x)=\frac{2}{x} ; u=4 \)
c) \( f(x)=\sin (x) ; u=0 \)
Ansatz:
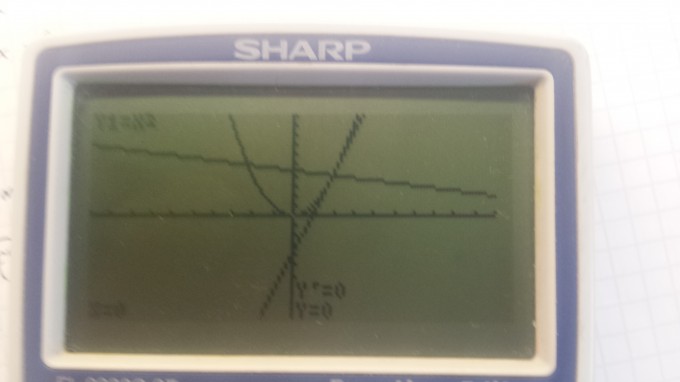
Ich habe hier die 1a) gerechnet. Die Tangente scheint bei X2 auch richtig zu sein aber die normale nicht. Was mach ich falsch? Die Normale müsste ja senkrecht zur Tangente stehen.
Tangentengleichung:
\( y=f^{\prime}(v) \cdot(x-v)+f(v) \quad f(x)=x^{2} \)
\( y=2 \cdot 2 \cdot(x-2)+2^{2} \quad f^{\prime}(x)=2 x \)
\( y=4 \cdot(x-2)+4 \)
\( y=4 x-8+4 \)
\( y=4 x-4 \)
Normale:
\( y=-\frac{1}{f^{\prime}(v)} \cdot(x-v)+f(u) \)
\( y=-\frac{1}{2 \cdot 2} \cdot(x-2)+2^{2} \)
\( y=-\frac{1}{4} x+\left(-\frac{1}{4} \cdot(-2)\right)+4 \)
\( y=-\frac{1}{4} x+\frac{1}{2}+4 \)
\( y=-\frac{1}{4} x+4 \frac{1}{2} \)