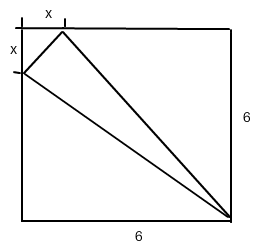
Einem Quadrat mit der Seitenlänge 6m soll ein gleichschenkliges Dreieck so einbeschrieben werden, dass eine seiner Ecken mit einer Quadratecke zusammenfällt. Wie lang sind die Seiten des Dreiecks zu wählen, damit sein Flächeninhalt maximal wird?
Meine Rechnung:
A = 36 - x2 /2 - 6 * (6 - x)
-1/2 (x-6)2 + 18, S (6/18)
Die Hypotenuse sollte √72 betragen, die Dreiecksschenkel 6m.
Maximaler Flächeninhalt A = 18m2 (??)
Danke für Hilfe
Sophie