Aufgabe Flächenschwerpunkt, Symmetrie, Integration:
Berechnen Sie für das gezeichnete Dreieck die Schwerpunktskoordinate \( x_{S} \). (Wegen der Symmetrie gilt \( y_{S}=0 \) ). Es gilt allgemein
\( x_{S}=\frac{1}{A} \int \limits_{A} x \mathrm{~d} A \)
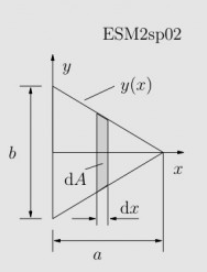
Gegeben: \( a, b \)
Lösung:
\( x_{S}=\frac{1}{A} \int \limits_{A} x \mathrm{~d} A=\frac{2}{b a} \int \limits_{0}^{a} x 2 y(x) \mathrm{d} x \). mit \( y(x)=\frac{b}{2}\left(1-\frac{x}{a}\right) \)
\( =\frac{2}{b a} \int \limits_{0}^{a} x b\left(1-\frac{x}{a}\right) \mathrm{d} x=\frac{2 b a^{2}}{b a} \int \limits_{0}^{a} \underbrace{\frac{x}{a}}_{\zeta}\left(1-\frac{x}{a}\right) \frac{\mathrm{d} x}{a} \)
\( = 2 a \int \limits_{0}^{1}\left(\zeta-\zeta^{2}\right) \mathrm{d} \zeta=2 a\left|\frac{\zeta^{2}}{2}-\frac{\zeta^{3}}{3}\right|_{0}^{1} \)
\( x_{S}=2 a\left(\frac{1}{2}-\frac{1}{3}\right)=\frac{a}{3} \)
Problem:
Ich habe die Lösung, eigentlich relativ einfach, allerdings verstehe ich einen Schritt (rot makiert) der Lösung nicht. Wurde hier die ganze Gleichung erweitert? Kann mir jemand dazu noch einen Zwischenschritt posten, sodass ich dass nachvollzeihen kann?