Krümmung und Steigung anhand Zeichnung erkennen

Question

habe eine Frage, ob ich dass richtig verstanden haben:

Wir rechnen momentan mit Funktionen und deren Ableitungen, um somit Steigung und Krümmung der ursprünglichen Funktion zu erkennen.

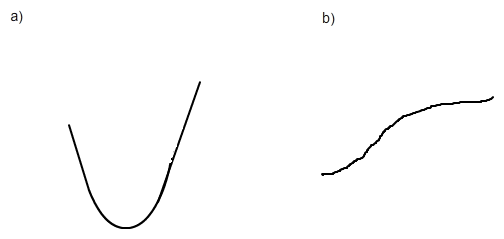
Muss ich bei dem Beispiel hier jetzt schreiben bei a) links vom Tiefpunkt rechtsgekrümmt und fallend, nach dem Tiefpunkt linksgekrümmt und steigend? und bei b) (erkennt man vielleicht nicht so genau an der zeichnung) dann genauso? vor dem Wendepunkt linksgekrümmt und steigend, nach dem Wendepunkt rechtsgekrümmt und steigend?

Danke schonmal,

LG meghan16

Answer 1

im Grunde schon nur:

a) Die Krümmung ist stets linksgekrümmt (es handelt sich um eine nach oben geöffnete Parabel, ihr werdet sehen, dass die zweite Ableitung einer solchen eine konstante positive Zahl ist).

b) ist richtig.

Noch was zur Krümmung (falls dies noch ein wenig unklar ist): Stell dir vor der Graph der Funktion ist eine Straße auf einer Karte und du fährst sie von links nach rechts entlang. In die Richtung in die du lenken musst um auf der Straße (also dem Graphen) zu bleiben ist stets die Richtung deiner Krümmung.

Gruß

Comments

Ah, das mit dem Auto fahren ist ein guter Tipp, danke :)

Die Steigung hat soweit aber gepasst oder?

---

Ja die Steigung hast du richtig erkannt :)

Answer 2

Steigend oder fallend hast du bei beiden Beispielen richtig erkannt.
a.)
Die Kurve ist komplett linksgekrümmt.
Du folgst der Kurve von links nach rechts ( auf der gedachten
x-Achse ). Die Kurve krümmt sich im Verlauf stets nach links.
b.)
Die Kurve ist zunächst linksgekrümmt.
Wechselt dann nach rechtsgekrümmt.
Dazwischen liegt der Wendepunkt.
Am Ende ist bei dir noch eine kleine
Linkskrümmung zu sehen ( falls so geplant ).

Comments

am Ende sollte keine mehr sein ja^^

ok, dann danke ich euch :)