Um den x-Wert zu finden, bei dem das einbeschriebene Rechteck maximalen Flächeninhalt hat, macht man sich die Eigenschaft der 1. Ableitung zu nutze, mit der man Extrempunkte von Funktionen ermitteln kann. Dazu setzt man die 1. Ableitung 0. Man löst die Gleichung nach x auf.
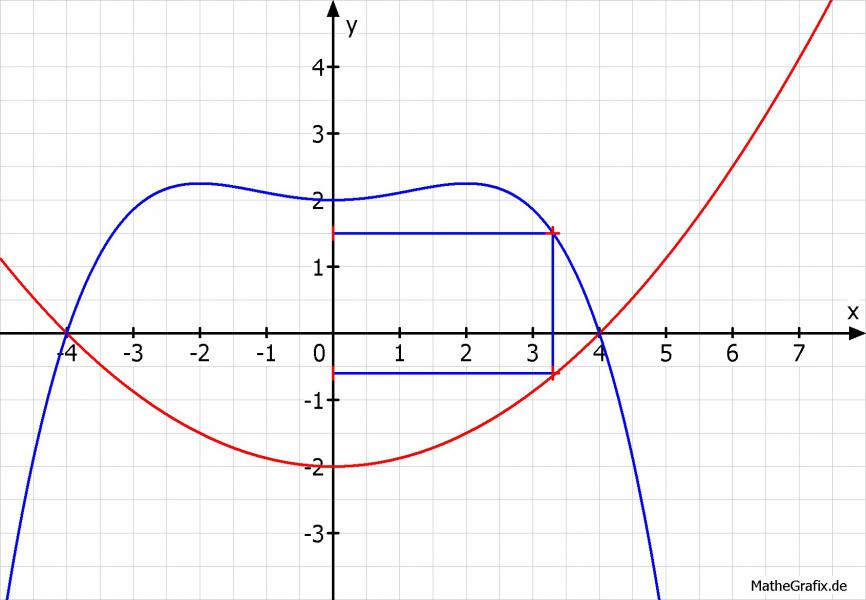
Nach dem das bekannt ist, muss man eine Funktion aufstellen, mit der man den Flächeninhalt des einbeschriebenen Rechtecks bestimmen kann. Hier ist das x mal die Differenz der Funktionen f(x) - g(x) (blau: f(x), rot : g(x) ). Die Differenz liefert die Länge der Kante parallel zur y-Achse, x die Länge der Kante parallel zur x-Achse.
Die Fläche eines Rechtecks ist das Produkt der Seitenlängen.
Da die Funktionen symmetrisch zu y-Achse sind wird hier nur der rechte Teil betrachtet. Das Ergebnis ist das selbe.
h(x) = ( f(x) - g(x) ) * x = -1/64 * x^5 + 4x
h'(x) = -5/64 * x^4 + 4 = 0
x1 = +4 / 5^{1/4}
x2 = - 4 / 5^{1/4}