Ermitteln Sie die Gleichung der Tangente an g, wenn der Übergang an x=-2 erfolgt. (Wellness-Liege Funktionsberechnung)

Question

Aufgabe:

Im "WOLF-RENZ_DESIGN_ZENTRUM" wird eine neue Generation an Wellness-Liegen entwickelt. Für das Topmodell „ABI 2006" haben die Designer geschickt Ausschnitte aus verschiedenen Funktionsgraphen zusammengesetzt.

a) Die Fußstütze ergibt sich als Verlängerung (Teil der Tangente) an das Gestell/Beinauflage g, wobei für g die Gleichung \( g(x)=\frac{1}{4} e^{x} \cdot(x-2)^{2} \) gilt.

a1) Weisen Sie nach, dass für die 1. Ableitung von g gilt: \( g^{\prime}(x)=\frac{1}{4} e^{x} \cdot\left(x^{2}-2 x\right) \).

a2) Ermitteln Sie die Gleichung der Tangente an g, wenn der Übergang an \( x=-2 \) erfolgt.

a3) Geben Sie den Bereich für \( \mathrm{x} \) an, in dem die Tangente als Fußstütze genutzt werden kann.

Answer 1

Hi Albert :-)

a1)

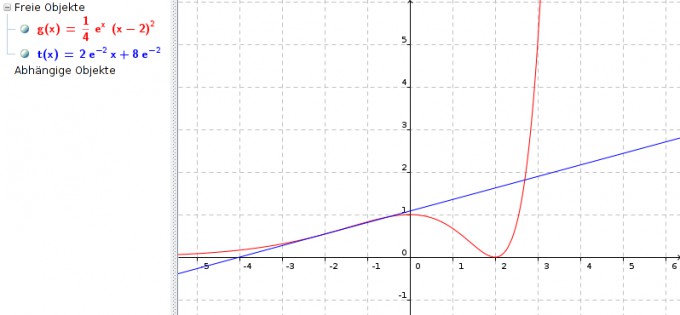
g(x) = 1/4 * e^x * (x - 2)²

Produktregel (f*g)' = f'g + fg'

(1/4 * e^x)' = 1/4 * e^x 

((x - 2)²)' = (x² - 4x + 4)' = 2x - 4

Demnach ist

g'(x) = 1/4 * e^x * (x - 2)² + 1/4 * e^x * (2x - 4) =

1/4 * e^x * [(x - 2)² + 2x - 4] =

1/4 * e^x * (x² - 4x + 4 + 2x - 4) =

1/4 * e^x * (x² - 2x)

a2)

Die Tangente an g hat an der Stelle x = -2 den gleichen Anstieg wie g:

g'(-2) = 1/4 * e^-2 * (4 + 4) = 2 * e^-2

Die Tangente an g hat an der Stelle x = -2 auch den gleichen Funktionswert wie g:

g(-2) = 1/4 * e^-2 * (-2 - 2)² = 1/4 * e^-2 * 16 = 4 * e^-2

Geradengleichung allgemein: y = m * x + b

4 * e^-2 = 2 * e^-2 * (-2) + b

b = 4 * e^-2 + 4 * e^-2 = 8 * e^-2

Damit lautet die Tangentengleichung

t(x) = 2 * e^-2 * x + 8 * e^-2

 

a3)

Bereich, in dem die Tangente als Fußstütze benutzt werden kann, ist wohl von ihrer Nullstelle bis zu x = -2.

t(x) = 2 * e^-2 * x + 8 * e^-2 = 0

2 * e^-2 * x = - 8 * e^-2 | : e^-2

2x = - 8

x = -4

Der Bereich ist also von x₁ = -4 bis x₂ = -2

Besten Gruß