Drachenviereck Textaufgabe mit Sinus, Kosinus und Tangens. Wie groß sind f, e, β, γ und δ?

Question

Aufgabe:

Von einem Drachenviereck \( \mathrm{ABCD} \) seien die Seitenlängen \( a=3,5 \mathrm{~cm} \) und \( b=6.5 \mathrm{~cm} \), ferner die Winkelgröße \( \alpha=88° \) bekannt.

Wie groß sind \( \mathrm{f}, \mathrm{e}, \beta, \gamma \) und \( \delta \) ?

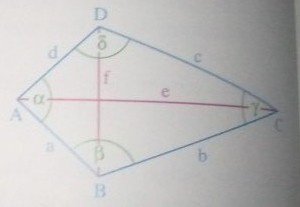
Ansatz/Problem:

Wie kann ich die Aufgabe lösen, es gibt kein 90° Winkel. Außer man teilt es auf, aber dann geht es ja auch nicht, weil so viele Sachen fehlen.

Answer 1

Beim Drachenviereck schneiden sich die Diagonalen im rechten Winkel. Rechne also die Dreiecke aus und du hast dann auch das Drachenviereck.

Zuerst

3.5 * SIN(88/2) = ...

3.5 * COS(88/2) = ...

Jetzt das danebenliegende Dreieck.

Schaffst du es selber ?

Comments

Ok, danke, habe diese Lösungen jetzt raus: 


f = 4,8
e = 4,9
ß = 46° * 2 = 92°

y= 45° * 2 = 90°

G = 44° * 2 = 88°

---

f stimmt näherungsweise. e ist allerdings schon nicht richtig.

Answer 2

Es soll ja wohl e die Symmetrieachse sein
Nenne den Schnittpu. der Diagonalen mal S.
Dann kennst du im Dreieck ABS den Winkel bei A
das ist dann eben 44° denn das ist ja   die Hälfte von alpha.
und du hast Seite AB und bei S einen rechten Winkel, dann
ist  sin(a) = BS / AB  damit kannst du BS ausrechnen und das ist
ja die Hälte von f 
mit cos bekommst du das Stück von A nach S.
Im Dreieck BCS hast du jetzt BC und SB  und den rechten Wi. bei S
damit kommst du weiter.