Extremwertaufgabe Kegel in Kegel einbeschreiben

Question

wir haben eine Aufgabe auf bekommen und ich habe absolut kein Plan!

Vielleicht kann mir ja mal jemand helfen.

Aufgabe lautet: Einem Kegel mit dem Radius r und der Höhe h soll ein zweiter Kegel so einbeschrieben werden, dass dessen Spitze im Mittelpunkt des Grundkreises liegt und sein Rauminhalt möglichst groß wird.Welches gleichschenklige Dreieck vom Umfang U hat den größten Flächeninhalt? Wahrscheinlich muss ich da mit Variablen arbeiten, da keine Zahlen vorgegeben sind.

 

bitte um Hilfe

Answer 1

Zu 2)
Bezeichne die Grundlinie des gleichschenkligen Dreiecks mit  a, die Schenkel mit  s  und die Höhe auf  a  mit  h.
Es gilt  u = a + 2s, also  a = u - 2s. Nach Pythagoras gilt
h² = s² - (a/2)² = s² - (u/2 - s)² = (u/4)·(4s - u).
Die Fläche berechnet sich aus  A = a·h/2.
Quadrieren ergibt  A² = a²·h²/4. Also ist
A²(s) = (u - 2s)²·u·(4s - u)/16 = (u/16)·F(s), wobei  F(s) := 16s³ - 20us² + 8u²s - u³.
Wenn  F  maximal ist, ist auch  A  maximal.
F'(s) = 48s² - 40us + 8u².
F'(s) = 0 ⇒ s = u/2 ∨ s = u/3.
Für  s = u/2  ist  a = 0.
Für  s = u/3  ist  a = u/3 = s.
Der Flächeninhalt ist also maximal, wenn es sich um ein gleichseitiges Dreieck handelt.

Comments

Ich danke vielmals!!! Ich versuche es jetzt mal nachzuvollziehen :-) eine Frage habe ich dennoch , bin neu hier und zwar z. B u/ 2 meinst Du damit u durch 2? Ich weiß eine doofe Frage

---

Ja, genau. u/2 bedeutet soviel wie u geteilt durch 2 oder u-Halbe (je nachdem, was Du vorziehst).

Du  musst bei dieser Schreibweise aber vorsichtig sein; wenn Du nämlich einen Bruch schreiben möchtest, sagen wir 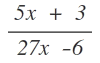, dann musst Du das so schreiben: (5x + 3) / (27x -6 ). Wenn Du das anders machst nämlich 5x + 3 / 27x - 6, dann steht da 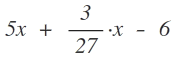. Das wird gern falsch gemacht. Also im Zweifelsfall ein paar Klammern mehr, als ein paar zu wenig.

Halte Dich am besten an die Regel Punkt- vor Strichrechnung, dann kann eigentlich nichts passieren und wenn was unklar ist, dann einfach fragen.  :)

---

Eine Antwort mit Zahlen findest du ev. hier:

https://www.mathelounge.de/2831/extremwertaufgabe-kreiskegel-kreiskegel-einzuschreiben