Ein 32 m großer Turm ist 64 m vom Ufer eines Flusses entfernt. Wie breit ist der Fluss?

Question

Aufgabe:

Ein 32 m großer Turm ist 64 m vom Ufer eines Flusses entfernt. Von der Spitze des Turms erscheint die Flussbreite unter einem Sehwinkel von 4,8°. Wie breit ist der Fluss an dieser Stelle?

Thema: Rechtwinkliges Dreieck, Sinus, Cosinus, Tangens

Comments

Ja. Eine gute Idee ist sich eine Skizze zu machen? Schaffst du das alleine? Du hast durch die angaben schon ein rechtwinkliges Dreieck mit gegebenen Katheten. In dem Dreieck kannst du also alles ausrechnen. Dann hast du ein anliegendes allgemeines Dreieck. Das berechnest du danach.

Answer 1

man braucht en kompletten winkel an der Turmspitze.

α+α₁=4,8°+x

tan (64 m / 32 m) = 63,43^°         ⇒   x=63,43°  (siehe auch Grafik unten)

α+α₁= 4,8° + 63,43° = 68,23°

Damit kann man jetzt 64+x berechnen, x ist die Breite des Flussees:

tan (68,23°) = (64+x )/32

            2,5 = (64+x)/32    |*32

          80,15 = 64+x        | -64

           16,15 = x    

Der Fluß ist 16,15m breit.( Es wurde gerundet)

   

Answer 2

Kleine, nicht maßstabsgetreue Skizze:

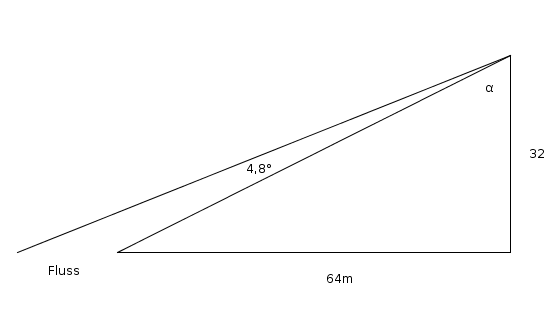
Meine Rechnung:

tan(α) = 64/32 = 2 | α = arctan(2) ≈ 63,4°

α' = 63,4° + 4,8° = 68,2°

tan(68,2°) = (64 + Flussbreite)/32

Flussbreite = tan(68,2°) * 32 - 64 ≈ 16

Der Fluss ist ca. 16 m breit.

Kleine Abweichung von Unknowns Ergebnis, weil dieser für α 2 Stellen nach dem Komma berücksichtigt hatte und ich nur eine :-)

Comments

Habe nur 2 Kommastellen genannt, aber exakt gerechnet.

Normal wird nur das Endergebnis gerundet^^.

---

Was bedeutet exakt gerechnet? 8 Stellen?

---

Da musst Du Texas Instruments fragen. Aber mit Sicherheit genauer.

Answer 3

Hi,

eine Skizze zum Veranschaulichen des Sachverhalts:

 

Du kannst direkt α berechnen:

tan(α) = 64/32 = 2

-> α = 63,43°

Nun den Winkel ß hinzunehmen (die 4,8°).

tan(α+ß) = (x+64)/32

x = 32tan(α+ß) - 64

x = 16,147 m

 

Der Fluß ist also etwa 16m breit.

 

Grüße