2^3*x^3*(1/2x+2/3+1/(9x))^3=1
richtig ausmultipliziert ergibt
x^6+4x^5+6x^4+112/27x³+4/3x²+16/81x+8/729 =1
x^6+4x^5+6x^4+112/27x³+4/3x²+16/81x-721/729=0
Die reelle Lösung ist mit der Abkürzung
(x^2 + 4/3x + 2/9)^3 = 1 | beide Seiten 3. Wurzel
x^2 + 4/3x-7/9=0 -> pq-Formel...
x1/x2= (-2 +/- sqrt(11))/3 schnell gefunden
ABER Gleichungen 6. Grades haben auch 6 Nullstellen:
Polynomdivision für die restlichen 4, wenn Ihr komplexe Zahlen schon hattet:
(x^6+4x^5+6x^4+112/27x³+4/3x²+16/81x-721/729)/(x+2/3-sqrt(11)/3)/(x+2/3+sqrt(11)/3)
=(x^6+4x^5+6x^4+112/27x³+4/3x²+16/81x-721/729)/(x²+4/3x-7/9)
=x^4+8/3x³+29/9x²+52/27x+103/81
Die 4 Nullstellen z.B. per pqrst-Formel (kein Schulstoff!):
(-4 +/-sqrt(2 (-5 +/-9 i sqrt(3))))/6
Beide kann man per http://www.lamprechts.de/gerd/php/gleichung-6-grades.php
überprüfen:
a) nur Teil2 also Grad 4 für x3...x6:
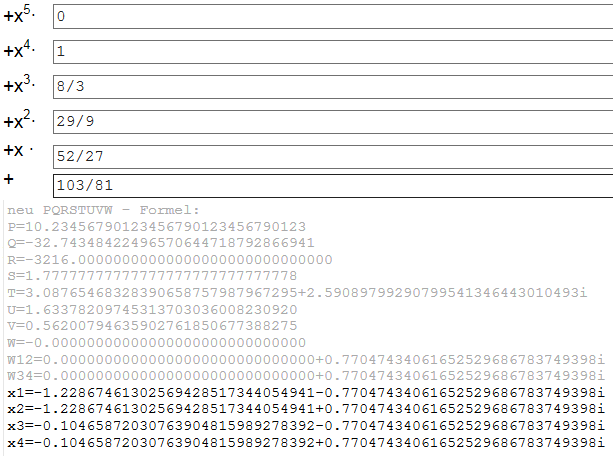
b) oder auch gleich alles zusammen Grad 6 für x1... x6:
