Finden Sie (mit Nachweis) Infimum und Supremum der folgenden Teilmengen von ℝ

Question

Aufgabe:

Finden Sie (mit Nachweis) Infimum und Supremum der folgenden Teilmengen von \( \mathbb{R} ! \)

(i) \( \left\{\frac{|x|}{1+|x|} \mid x \in \mathbb{R}\right\} \)

(ii) \( \left\{\frac{n^{2}}{2^{n}} \mid n \in \mathbb{N}\right\} \)

(iii) \( \left\{x-\frac{1}{x^{2}} \mid x \in(1, \infty)\right\} \)

Answer 1

Grundsätzlich schaut man sich einfach die Grenzwerte und ggf ein paar Werte an, um zu Schauen, wie der dazugehörige Graph aussieht.

Für (i) zum Beispiel:

\( \lim \limits_{0} \frac{|x|}{1+|x|}=\frac{0}{1+0}=0 \)

\( \lim \limits_{\infty} \frac{|x|}{1+|x|}=\frac{\infty}{1+\infty}=1 \)

Der Graph selbst hat auch keine Wellen oder Ausreißer:

Also ist das Infimum = 0 und das Supremum = 1

Für (ii) gilt.

\( \lim \limits_{0} \frac{n^{2}}{2^{n}}=\frac{0}{1}=0 \)

\( \lim \limits_{\infty} \frac{n^{2}}{2^{n}}=\frac{n^{\infty}}{2^{\infty}}=0 \)

Der Graph sieht wie folgt aus:

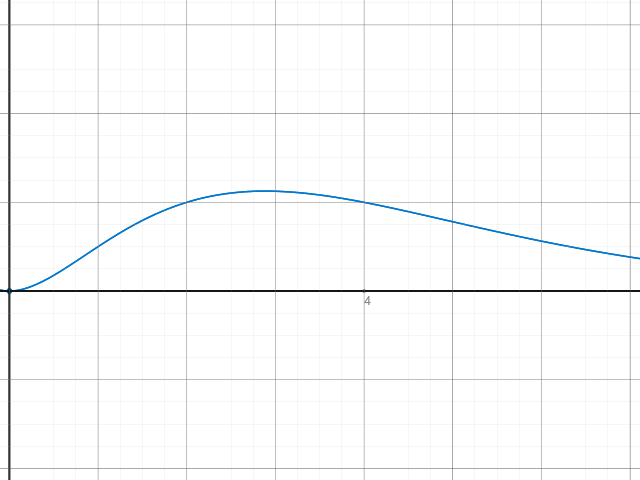
Anscheinend ist das Supremum bei x = 3.

\( \frac{3^{2}}{2^{3}}=\frac{9}{8} \)

Für (iii)

\( \lim \limits_{1} x-\frac{1}{x^{2}}=1-1=0 \)

\( \lim \limits_{\infty} \infty-\frac{1}{\infty^{2}}=\infty \)

Der Graph:

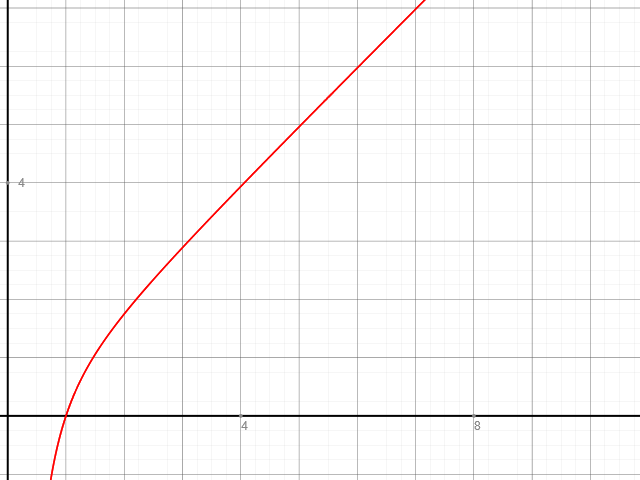
Also gibt es kein Supremum und das Infimum ist 0, da wir die Funktion nur bis x=1 betrachten.