hier: tan-1(x) = atan(x) = Umkehrfunktion
und nicht tan(x)^{-1} = 1/tan(x) = Kehrwert
geg.: exp(2*x+2)+2*atan(2*x)=0
ges.: x
Wie das funktioniert, zeigt der Iterationsrechner im Beispiel 118:
http://www.gerdlamprecht.de/Roemisch_JAVA.htm#ZZZZZ0118
Nur Funktion die Null werden soll und Startwert eingeben fertig:
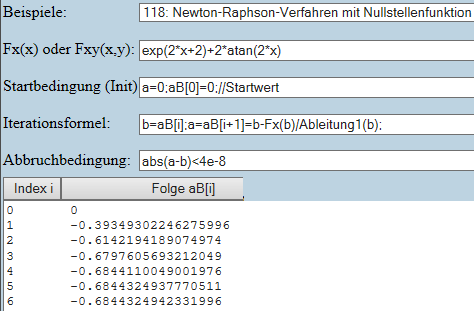
Statt Numerischer Ableitung, kann man auch Symbolisch ableiten, also Ableitung1 durch
d/dx = (2*exp(2+2*b)+4/(1+4*b*b)) mit b statt x, da hier b die Variable ist:
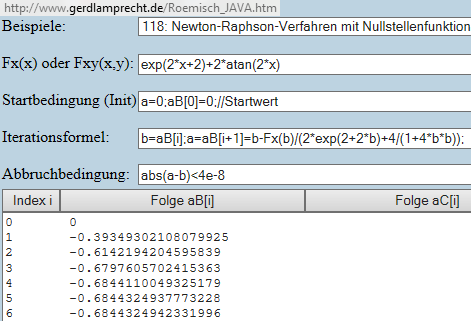
Nur minimale Unterschiede ab der 9. Nachkommastelle bei der 1. Iteration. Da Selbstkonvergenz vorliegt, gleicht sich das bis zur 6. Iteration selbst aus.
Grafische Probe:
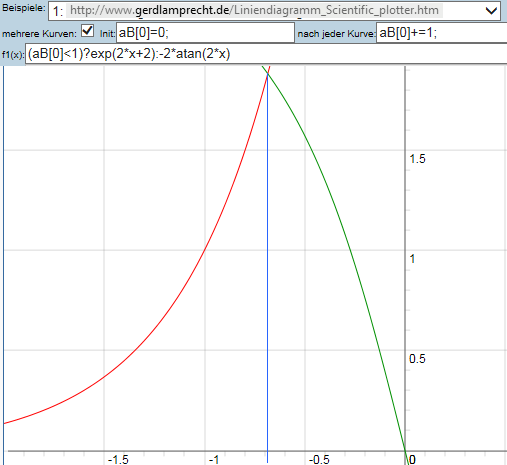
Alles OK.