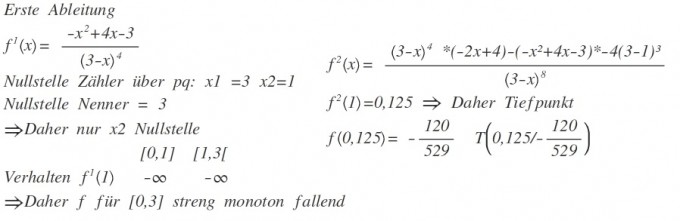Bestimmen Sie die Extremwerte und das Monotonieverhalten.
f [0,3[ -> R f(x) = x-2 / (3-x)
\( f:\left[0,3\left[\rightarrow \mathbb{R}, \quad f(x)=\frac{x-2}{(3-x)^{2}}\right.\right. \)
Ansatz:
Erste Ableitung
\( f^{l}(x)=\frac{-x^{2}+4 x-3}{(3-x)^{4}} \)
Nullstelle Zähler über pq:
\( x l=3 \quad x 2=1 \)
Nullstelle Nenner \( =3 \)
→ Daher nur \( x 2 \) Nullstelle \( {[0,1]} \quad {[1,3[} \) Verhalten \( f^{\prime}(1) \quad -\infty \quad -\infty \)
→ Daher f für [0,3] streng monoton fallend
\( [ 0 , 1 ] \quad [ 1 , 3 [ \\ \text { Verhalten } f ^ { \prime } ( 1 ) { - \infty } { - \infty } \)
→ Daher f für [ 0 , 3 ] streng monoton fallend
\( f^{2}(x)=\frac{(3-x)^{4} *(-2 x+4)-\left(-x^{2}+4 x-3\right)^{*}-4(3-1)^{3}}{(3-x)^{8}} \)
\( f^{2}(I)=0,125 \Rightarrow \) Daher Tiefpunkt
\( f(0,125)=-\frac{120}{529} \quad T\left(0,125 /-\frac{120}{529}\right) \)