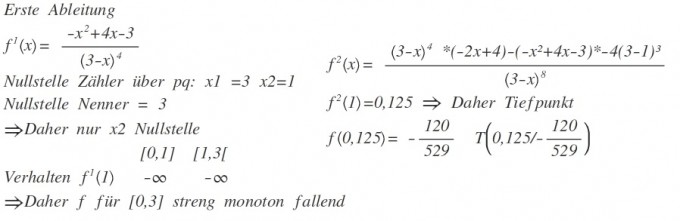Bestimmen Sie die Extremwerte und das Monotonieverhalten von f(x)=(x-2)/(3-x)2

Question

Bestimmen Sie die Extremwerte und das Monotonieverhalten.

f [0,3[ -> R      f(x) = x-2 / (3-x)

$f:\left[0,3\left[\rightarrow \mathbb{R}, \quad f(x)=\frac{x-2}{(3-x)^{2}}\right.\right.$

Ansatz:

Erste Ableitung

$f^{l}(x)=\frac{-x^{2}+4 x-3}{(3-x)^{4}}$

Nullstelle Zähler über pq:

$x l=3 \quad x 2=1$

Nullstelle Nenner $=3$

→ Daher nur $x 2$ Nullstelle ${[0,1]} \quad {[1,3[}$ Verhalten $f^{\prime}(1) \quad -\infty \quad -\infty$
→ Daher f für [0,3] streng monoton fallend

$[ 0 , 1 ] \quad [ 1 , 3 [ \\ \text { Verhalten } f ^ { \prime } ( 1 ) { - \infty } { - \infty }$

→  Daher f für [ 0 , 3 ] streng monoton fallend

$f^{2}(x)=\frac{(3-x)^{4} *(-2 x+4)-\left(-x^{2}+4 x-3\right)^{*}-4(3-1)^{3}}{(3-x)^{8}}$

$f^{2}(I)=0,125 \Rightarrow$ Daher Tiefpunkt

$f(0,125)=-\frac{120}{529} \quad T\left(0,125 /-\frac{120}{529}\right)$

Answer 1

Nach dem Extrempunkt ist die Steigung positiv.
E ist Minimum

Comments

Frohes Neues an alle Matheexperten.

Danke. Kannst du mir erklären, warum in der dritten Zeile, dass ² von (3-x) wegfällt? Du kürzt doch schon mit (3-x). Außerdem ist es eine Summe.

Wie funktioniert deine Monotonierechnung?

Ich kenne nur  die beiden Verfahren:
a)
Erste Abl. Berechnen
Nullstellen der ersten Ableitung berechnen
Zweite Ableitung berechnen
Nullstellen der ersten Abl. in die zweite Abl. Einsetzen
Intervalle benennen

b)
Erste Ableitung berechnen
Nullstellen der ersten Ableitung berechnen
Intervalle benennen
Monotonietabelle aufstellen
Vorzeichen der Intervalle berechnen

---

Danke. Kannst du mir erklären, warum in der dritten Zeile, dass ² von (3-x)
wegfällt? Du kürzt doch schon mit (3-x). Außerdem ist es eine Summe.

Ein Term hoch 3 ist nur dann positiv wenn der Term selbst positiv ist.
Aus ( 3 - x )³ > 0  folgt ( 3 - x ) > 0

a.) und b.)
Um die Bildung der 2.Ableifung habe ich mich gedrückt.
Ich habe folgendes angewandt
1.Ableitung = 0 : Punkt mit waagerechter Tangente
1.Ableitung > 0 : Monotonie positiv = steigend
1.Ableitung < 0 : Monotonie negativ = fallend
Wenn ich einen Punkt mit waagerechter Teangente ermittelt habe und die
- Monotonie links des Punkt ist fallend und rechts steigend ist es ein Minimum
- Monotonie links des Punkt ist steigend und rechts fallend ist es ein Maximum
( Es gibt auch die Fälle Sattelpunkt, will ich jetzt aber nicht mehr darstellen )

Da die 1.Ableitung ein Bruch ist gilt
positiv / positiv ergibt vom Vorzeichen positiv
negativ / negativ ergibt vom Vorzeichen positiv
In diesen beiden Fällen wäre der Wert der 1.Ableitung positiv
1.Fall
( x - 1 > 0 ) und [ ( 3 -x )³ > 0 ]
x > 1 und x < 3
1 < x < 3
2.Fall
negativ durch negativ ergibt keine Schnittmenge

Jetzt könnte man noch untersuchen wann die 1.Ableitung
negativ ist
3.Fall : negativ durch positiv und
( x - 1 < 0 ) und ( ( 3 - x )³ > 0 )
4.Fall : positiv durch negativ
( x - 1 > 0 ) und (  ( 3 - x )³ < 0 )

Durch die Kenntnis der Monotoniebereiche kann
man nun beweisen von welcher Art der Extrempunkt ist.

---

Danke. Solche Tricks darf man man einfach anwenden?

Ich gestehe, dass mir deine Methode zu schwierig ist, aber mit der vereinfachten Ableitung sollte es auch mit dem Standardverfahren klappen.

---

Danke. Solche Tricks darf man man einfach anwenden?

Das ist kein Trick.

Die 1.Ableitung kann unter anderem auch dazu benutzt werden
Monotoniebereiche festzustellen. Eine mögliche Aufgabenstellung in Arbeiten
wäre : In welchen Intervallen ist die Funktion steigend bzw. fallend.

---

Ich hab das ganze nochmal neu ausgerechnet.

Von [0,1[ ist die Funktion monoton fallend

bei 1 liegt ein Tiefpunkt (1/0,25) vor

Von ]1,3[ ist die Funktion monoton steigend

Mir ist noch aufgefallen:

Du hattest geschrieben, dass:

" Ein Term hoch 3 ist nur dann positiv wenn der Term selbst positiv ist.
Aus ( 3 - x )³ > 0  folgt ( 3 - x ) > 0"

Aber in dem gekürzten Term ist kein hoch 3. Du machst ein (3-x)²  zu (3-x).

---

Du machst ein (3-x)²  zu (3-x)..

Nicht generell. Ich schließe
" aus ( 3 - x )³ > 0  folgt ( 3 - x ) > 0 "

Gehen wir umgekehrt vor :
3 - x > 0 | 3 - x ist also positiv. Daraus folgt :
wird der Term 3 mal mit sich selbst malgenommen ist das Ergebnis
auch positiv.
( 3 - x )³ > 0
[ Anmerkung : der Term kann beliebig oft mit sich selbst malgenommen
werden, das Ergebnis bleibt stets positiv. ]

Falsch wäre es zu behaupten
aus ( 3 - x )³ > 9  folgt ( 3 - x ) > 9

---

Gern geschehen.

  Hier, zur Aufheiterung, eine Anekdote über Albert Einstein ( wenn Sie nicht
wahr ist, dann ist sie gut erfunden )

  Albert Einstein hatte gerade seine spezielle Relativitätstheorie ausgetüftelt und war erst in Fachkreisen bekannt. Er bekam eine Einladung nach Amerika zu kommen und dort seine Theorie an Universitäten vorzustellen.

  Albert Einstein nahm das Angebot an, reiste nach Amerika und bekam u.a. einen jungen Doktoranten als Chauffeur zur Verfügung gestellt um ihn an die verschiedenen
Universitäten zu fahren.

  Nach ein paar Vorträgen sagte der Doktorant zu Einstein : " Herr Einstein, ich habe jetzt Ihren Vortrag mehrmals gehört und denke das ich die Theorie auch verstanden habe. Ich könnte die Theorie auch erklären. "

  Einstein war skeptisch. Es wurde aber ein Rollentausch vereinbart. Der Doktorant sollte den nächsten Vortrag halten, während Einstein sich unter die Zuhörer mischen würde. Der Vortrag wurde zur Zufriedenheit gehalten, danach konnten die Zuhörer noch Fragen stellen.

  Eine Frage war besonders kniffelig. Der Doktorant antwortete " Die Frage ist so
einfach " und zeigte auf Einstein " das Sie auch mein Chauffeur beantworten kann ".

---

Zwei Anmerkung am Rande:

(1) Das Betrachten von Ungleichungen der Form $f'(x) > 0$ oder $f'(x) < 0$ im Zusammenhang mit dieser Aufgabe ist – insbesondere nach der vorangegangenen Bestimmung der Extremstellen – völlig unnötig.

(2) "Doktorand" wird auch hinten mit "d" geschrieben!

---

@hh916
...insbesondere nach der vorangegangenen Bestimmung der
Extremstellen – völlig unnötig.

Ich habe meine Antworten nicht für dich sondern für den Fragesteller verfasst.
Ich hoffe es hat ein guter Lerneffekt stattgefunden.

Völlig unnötig - ist genau die richtige Bezeichnung für deinen Kommentar.

Am Besten du stellst demnächst eigene ANTWORTEN ein.

---

Hallo Georg!
In aller Ruhe und mit der immer gebotenen Sachlichkeit:

Die Aufgabe lautete:
Bestimmen Sie die Extremwerte und das Monotonieverhalten
der Funktion f: [0,3[ → ℝ mit f(x) = (x-2) / (3-x)!

Die Aufgabe besteht aus zwei Teilen:

Zunächst sollen die Extremwerte bestimmt werden. Da f in ihrem ganzen Definitionsbereich differenzierbar ist, finden sich die inneren Extremstellen unter den Nullstellen der ersten Ableitung. Die einzige Nullstelle x=1 der ersten Ableitung wurde bereits im Startbeitrag angegeben und als Tiefstelle charakterisiert. (Auf die Randextremstelle x=0 gehe ich hier nicht ein!)

Sodann soll das Monotonieverhalten bestimmt werden. Hier will der Aufgabensteller wissen, ob der Aufgabenbearbeiter die Ergebnisse des ersten Teils auch geeignet würdigen kann, ob er also weiß, dass die Tiefstelle x=1 die obere Grenze des fallenden und die untere Grenze des steigenden Monotoniebereichs ist. Hier müssen die Früchte des vorher Gesäten geerntet werden, Begründungen sind nicht mehr erforderlich.

Vor diesem Hintergrund halte ich Deinen Hinweis: "Die 1. Ableitung kann unter anderem auch dazu benutzt werden, Monotoniebereiche festzustellen. Eine mögliche Aufgabenstellung in Arbeiten wäre: In welchen Intervallen ist die Funktion steigend bzw. fallend.", sofern er sich auf das Lösen von Ungleichungen der Form $f'(x) > 0$ oder so beziehen sollte, für irreführend. Zur Identifikation von Monotoniebereichen bei Funktionen wie der vorliegenden ist es nicht erforderlich, Ungleichungen zu lösen.

Im Übrigen sind deine Betrachtungen zur Bedeutung der ersten Ableitung ja weder falsch noch uninteressant.

Ich hoffe, mein Einspruch ist nun ein wenig verständlicher geworden.

---

In aller Sachlichkeit.

Fragesteller : Ich würde gern wissen ob ich richtig gerechnet habe.

Die Antwort des Fragestellers ist voller Fehler. Das kannst du ja
selbst einmal überprüfen bzw. hättest du eigentlich schon tun sollen.

Ich habe mir daher die Antwort des Fragestellers nicht mehr weiter
angeschaut sondern eine eigene Antwort bezüglich Extremstelle
und Monotonie eingestellt.

Zudem habe ich auch noch die Art der Extremstelle begründet.

---

Mein Fehler lag darin, dass ich die Nullstelle ausversehen in die f(x)  eingesetzt habe.

Ansonsten geben beide Ableitungen dasselbe Ergebnis aus.

---

@ih127
Die in der Fragestellung angegebene Ableitung für f ´
ist richtig. Sie kann aber noch gekürzt werden. Dies ist
mittlerweile bekannt.
Die Extremstelle von x = 1 wurde von dir richtig bestimmt.

Nicht richtig ist die Aussage :
f ´ im Intervall [0..1] ist -∞
f ´ im Intervall [1..3] ist -∞
( falls ich deine Schreibweise so richtig gedeutet habe )

Richtig  ist
f ´ ( x ) im Intervall [0..1] ist negativ
f ´ ( x ) im Intervall [1..3] ist positiv

Daher für f im Intervall [0,3] streng monoton fallend.
Ist falsch.

Das ist alles nicht schlimm. Du hast dich ja hier an das Forum
gewandt um überprüfen zu lassen ob deine Berechnungen
richtig sind.

mfg Georg

---

Wir meinten beide dasselbe :-).

Ich würde dir gern den Stern geben, aber ich habe den ersten Beitrag auf einem anderen Computer verfasst. Anscheinend muss die IP stimmen.

Answer 2

f [0,3[ -> R      f(x) = x-2 / (3-x) = x- 2*(3-x)^-1

f ' (x) = 1 - (-1)*2*(3-x)^-2 * (-1) = 1 - 2/(3-x)²

Ich komme hier keinesfalls auf dein f ' .

EDIT: Dein erstes Bild wird bei mir nicht angezeigt.

Schau mal hier: https://www.wolframalpha.com/input/?i=+f%28x%29+%3D+x-2+%2F+%283-x%2…

Comments

Stimm da ist etwas schief gelaufen. f(x) ist $f:\left[0,3\left[\rightarrow \mathbb{R}, \quad f(x)=\frac{x-2}{(3-x)^{2}}\right.\right.$

---

Das sieht nun vernünftiger aus. Du kannst  damit dann gleich selbst kontrollieren.

https://www.wolframalpha.com/input/?i=+f%28x%29+%3D+%28x-2%29+%2F+%2…

https://www.wolframalpha.com/input/?i=%281-x%29%2F%28-3%2Bx%29%5E3&l…

---

Du hast im Zähler deiner Ableitung die Nullstelle 3 gefunden. D.h., dass du den Zähler faktorisieren kannst.

(3-x)*(x-1)

Da kannst du (3-x) dann noch wegkürzen und es bleibt

f ' (x) = (x-1) / (3-x)³

Das macht dann die Fortsetzung auch einfacher.

f ' (x) hat nur eine Nullstelle x = 1.

In den Intervallen [0,1] und [1,3) ist die Funktion monoton.

Teste einen Wert der Ableitung in jedem Intervall.

Du stellst fest

f ' (0.5) < 0

f ' (2) > 0

x = 3 ist eine vertikale Asymptote von f.

Fazit: Für 0 ≤x ≤ 1 ist der Graph von f monoton fallend, für 1 ≤x<3 ist der Graph von f monoton steigend.

---

Warum darf man  bei Nullstellen faktorisieren und warum ist f ' (2) > 0?

Ein Bruch mit negativem Zähler bleibt doch negativ.

---

"Ein Bruch mit negativem Zähler bleibt doch negativ." Auch wenn der Nenner negativ ist ?

---

Dann natürlich nicht. Ich erkenne nur nicht, wie man von meinem f ' auf dein f ' kommt.

---

Das habe ich dir oben ausführlich beschrieben.

Dein Zähler ist (3-x)*(x-1) = 3x - x² -3 + x  = -x² + 4x - 3

Dann kannst auch du kürzen.

Vermutlich hattest du einmal zu viel ausmultipliziert, wo du hättest ausklammern können.

---

Wenn du den Zähler von deinem f ' (2) ausrechnest, bekommst du -4 + 8 -3 = 1 > 0.

Und + / + gibt +.

Schreib bei Verhalten besser

f '(x) < 0 für 0≤x≤1 und f '(x) > 0 für 1≤x<3

Plus oder minus UNENDLICH sind dort irreführend.

EDIT: Habe in der Fragestellung dein Bild eingefügt und das Feld, das nicht dargestellt wurde, entfernt. Bilder im Formal .png werden richtig dargestellt.