Kegelschnitt - Ellipse?

Question

Ein Sachverhalt beim Kegelschnitt könnte für mich einmal geklärt
werden.

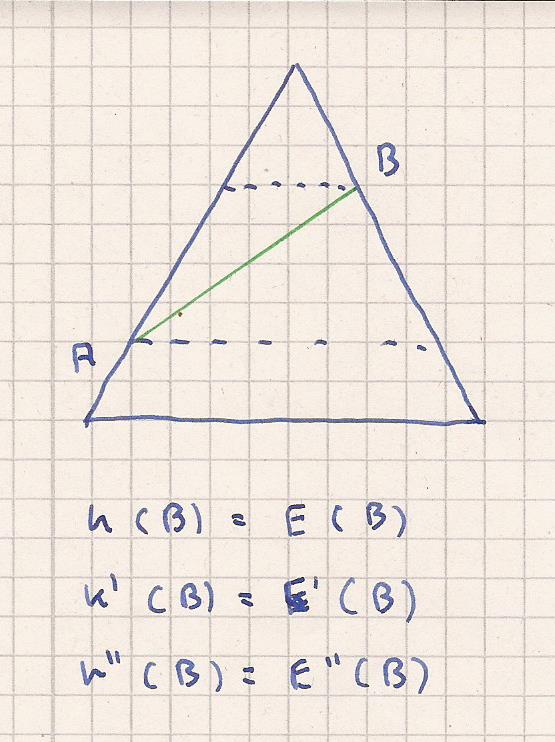
Die erste Skizze zeigt einen Kegel.
Nun wird vom Punkt B nach Punkt A der Kegel zerschnitten.
Es entsteht eine Ellipse.
Die gestrichelte Linie oben und unten wären zwei waagerechte
Kegelschnitte die 2 Kreise ergeben würden.

Die 2.Skizze zeigt die Draufsicht. 

Nun vermute ich einmal das gilt
( K = Kreisgleichung, E = Ellipsengleichung )
K ( B ) = E ( B )
K ´( B ) = E ´( B )
K ´´( B ) = E ´´( B )

Dasselbe für den Punkt A.

Die zweite Gleichung = Gleichheit der Krümmung
Dies dürfte aber nicht gegeben sein, da der Radius des
oberen Krümmungskreises kleiner ist als der untere.

Also müßte die Ellipse unsymmetrisch bezüglich Ihrer
Gestalt in Richtung x-Achse sein.

Wer weiß es ?

Answer 1

Das mit den Krümmungskreisen stimmt so wohl nicht; denn die Ellipse verläuft ja in einer Ebene, die gegen die Ebenen der Kreise geneigt ist. Damit die Krümmungen übereinstimmen, müssen aber die Krümmungskreise in der gleichen Ebene verlaufen, wie die betrachtete gekrümmte Linie.

Comments

Hallo mathef,
dies waren auch schon einmal meine Gedanken aber :

es  besteht doch ein erheblicher   ( scheinbarer ) Unterschied
zwischen bei beidem Krümmungskreisen, ( Nur scheinbar ? )
Die Frage beschäftigte  mich damals in der Schulzeit schon
als Kegelschnitte durchgenommen wurden.

Von Gefühl her erschien mir die Ovalform ( z.B. eines Ei´s )
logischer als die symmetrische Ellipse.

---

Keiner der beiden Kreise ist ein Krümmungskreis der Ellipse in dem gemeinsamen Punkt.

Stell dir doch mal eine Parabel im xy-Koordinatensystem vor und einen Kreis in der

x2x3-Ebene, der durch (0/0/0) verläuft. dann wäre der ja unabhängig vom Radius immer ein

Krümmungskreis der Parabel. Dem ist aber nicht so.