Kreis Fläche berechnung und Umfang

Question

Aufgabe - Vier kongruente Kreise mit dem Radius r = 7 cm schneiden sich im Punkt M. Ihre Mittelpunkte A, B, C und D sind Eckpunkte eines Quadrats. Der große Kreis mit Mittelpunkt M berührt die vier Kreise.

Rechnen Sie mit π = \( \frac{22}{7} \) !

Berechnen Sie

a) den Umfang der gefärbten Figur!

b) den Flächeninhalt der gefärbten Figur!

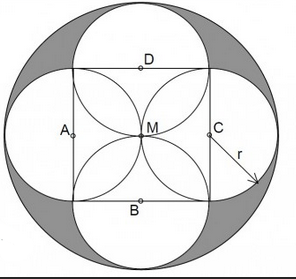
Ich komme bei der Aufgabe immer auf das falsche Resultat kann mir jemand erklären bzw. zeigen wie man das richtig rechnet?

Meine "falsche" Lösungen sind bei:

a) = 88cm

b) = 266cm²

Answer 1

ich hätte jetzt die Fläche vom großen Kreis - die Fläche vom Quadrat - 4 Halbkreise (= 2 ganze Kreise) gerechnet. (Ergebnis folgt)

Wie hast du es denn gemacht?

Comments

a) 14*2*pi

b) oh jetzt sehe ich den rechen Fehler bei Aufgabe B)

Kannst du mir Aufgabe a erklären ?

---

also habe bei a) 176 cm und bei b) 112 cm² raus

du muss bei a) erstmal den Umfang des großen Kreis ausrechnen (=88cm) - den halben Umfang von den 4 kleinen Kreisen (= 2* der Umfang von einem ganzen kleinen Kreis) (= 88cm) und die beiden Ergebnisse muss du dann noch zusammenziehen, soll ich nochmal die kompletten Rechnung aufschreiben?

---

wäre dir sehr dankbar für die ganze rechnung

---

dein Fehler bei a) war das du vergessen hast die "Zwischenräume" mit Abzuziehen

---

Beim grossen Kreis ist doch:

Radius= 14 cm

und der Umfang eines Kreises rechnet man doch mit Radius * 2 * pi

---

das ist jetz die a) die b) auch?

---

b) ist nun klar

aber wieso rechnest du bei a noch einen kleinen kreis?

---

Mal dir am besten mal an wo der Umfang von der gefärbten Fläche ist (krieg das am PC jetzt grade nicht so hin) Dann siehst du das Innerne, also an den Rändern der vier kleinen Kreise, auch beinhaltet. alo musst du den Umfang der vier kleinen Halbkreise auch mit berechnen.

Umfang_{gefärbte Fläche}= Umfang_{großer Kreis} + Umfang_{4* kleine Halbkreise}

---

Meinst du das rote? mit den kleinen kreisen?

---

ja genau! Um den Umfang der gefärbten Fläche zu erhalten, musst den Umfang der rote und der grüne Fläche zusammenziehen