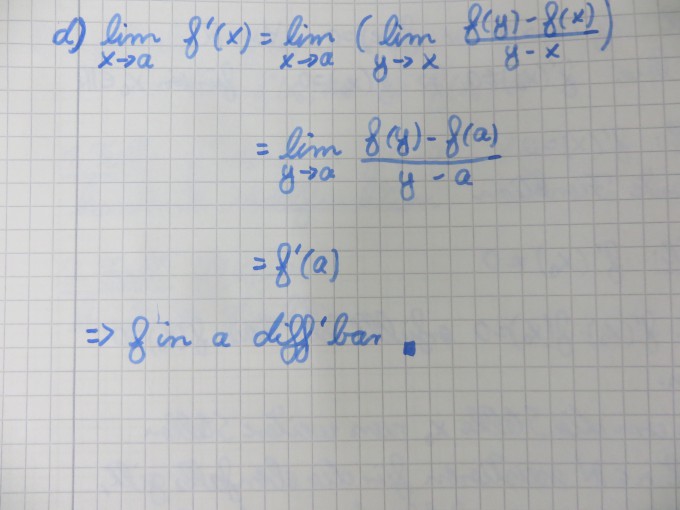Aufgabe:
a) Seien \( n \in \mathbb{N}, n \geq 2, a, b \in \mathbb{R} \) und \( f: \mathbb{R} \rightarrow \mathbb{R}: x \mapsto x^{n}+a x+b \). Zeigen Sie, dass \( f \) höchstens 2 Nullstellen hat, wenn \( n \) gerade ist.
b) Sei \( f \) eine auf \( \mathbb{R} \) differenzierbare Funktion mit der Eigenschaft \( f^{\prime}(x) f(x)=0 \) für alle \( x \in \mathbb{R} \). Zeigen Sie, dass \( f \) konstant ist.
c) Sei \( f:] a, b\left[\rightarrow \mathbb{R}\right. \) differenzierbar mit beschränkter Ableitung \( f^{\prime} \). Zeigen Sie, dass \( f \) gleichmäßig stetig ist.
d) Sei \( f:[a, b] \rightarrow \mathbb{R} \) stetig, auf \( ] a, b\left[\right. \) differenzierbar und \( \lim \limits_{x \rightarrow a} f^{\prime}(x) \) existiere. Zeigen Sie, dass \( f \) in \( a \) differenzierbar ist und dass \( f^{\prime}(a)=\lim \limits_{x \rightarrow a} f^{\prime}(x) \) gilt.
Ansatz/Problem:
Ich habe für die a), b) und d) bereits eine Lösung, bin mir allerdings nicht sicher, ob das so stimmt. Wenn mal jemand drüberschauen könnte, wäre das nett. Besonders die d) kommt mir etwas zu einfacht gelöst vor. Zur c) ist mir noch nichts eingefallen, weswegen es gut wäre, wenn mir jemand einen Tipp zur c) geben könnte (keine Lösung).
Meine Lösungen: