Produktionsfunktion x=f(r1 ; r2)=4r10.6 r20,5

Question

Gegeben sei die Produktionsfunktion x=f(r1 ; r2)= 4 r1^0,5 r2^0,6. Die Beschaffungspreise der Produktionfaktoren betragen 4 GE für eine Einheit von Inputfaktor r1 und 5 GE für eine Einheit von Inputfaktor r2.

a. Welche maximale Produktionsmenge kann erreicht werden, wenn ein Kostenbudget in Höhe von 44 GE vorhanden ist?

b. Bestimmen sie mittels der impliziten Ableitung dr2/dr1 und ermitteln sie die Steigung im Optimalpunkt.

Ich bitte um Hilfe beim Lösen dieser Aufgabe. Teilaufgabe a hatten wie in ähnlicher Form in der Schule mit Matrizzen, nun allerdings mit Exponenten, von denen ich nicht weiß wie ich sie behandeln soll. Von der impliziten Ableitung habe ich offen gestanden bis zum heutigen noch nie etwas gehört, unsere Dozentin war aber der Meinung, dass so etwas bereits Thema im Mathe GK sei.

Ich bedanke mich schon einmal im Voraus für Hilfe und hilfreiche Anmerkungen.

Answer 1

Gegeben sei die Produktionsfunktion x=f(r1 ; r2)= 4 r1^0,5 r2^0,6. Die
Beschaffungspreise der Produktionfaktoren betragen 4 GE für eine
Einheit von Inputfaktor r1 und 5 GE für eine Einheit von Inputfaktor r2.

a. Welche maximale Produktionsmenge kann erreicht werden, wenn
ein Kostenbudget in Höhe von 44 GE vorhanden ist?

f ( r1, r2 ) = 4 * r1^0.5 * r2^0.6
4 * r1 + 5 * r2 = 44
5 * r2 = 44 - 4 * r1
r2 = ( 44 - 4 * r1 ) / 5
f ( r1 ) = 4 * r1^0.5 * (( 44 - 4*r1 ) / 5 )^0.6

Ich sehe gerade das du die Exponenten ( 0.5 / 0.6 ) mal ( 0.6 / 0.5 )
angegeben hast. Bevor ich losrechne muß das geklärt werden.
Ansonsten 1.Ableifung bilden.
Zu 0 setzen und den Extremwert berechnen.

Comments

Danke erst mal für die Bemühungen.

Die Produktionsfunktion lautet 4r1^0,6  r2^0,5, mein Fehler.

Die 4 zu Beginn der Funktion hat allerdings nichts mit den 4 GE für Inputfaktor r1 zu tun sondern ist einfach nur ein Faktor.

---

f ( r1 ) = 4 * r1^0.6 * (( 44 - 4*r1 ) / 5 )^0.5

f ( r1 ) = 4 * r1^0.6 *  ( (44/5)^0.5   - 4/5 *r1^0.5 )

u = r1^0.6
u´ = 0.6 * r1^-0.4
v = ( (44/5)^0.5   - 4/5 *r1^0.5 )
v ´=  - 4/5*0.5 *r1^-0.5 ) = -0.4 * r1^-0.5

f ´( r1 ) = 4 * [ 0.6 * r1^-0.4 * ( (44/5)^0.5   - 4/5 *r1^0.5 ) + r1^0.6 * (-0.4) * r1^-0.5 ]

4 * [ 0.6 * r1^-0.4 * ( (44/5)^0.5   - 4/5 *r1^0.5 ) + r1^0.6 * (-0.4) * r1^-0.5 ] = 0
0.6 * r1^-0.4 * ( (44/5)^0.5   - 4/5 *r1^0.5 ) + r1^0.6 * (-0.4) * r1^-0.5  = 0

Jetzt wird es zuviel. Selbst mein Matheprogramm schafft es nicht.

Die Funktion f ( r1 ) = 4 * r1^0.6 * (( 44 - 4*r1 ) / 5 )^0.5  als Graph

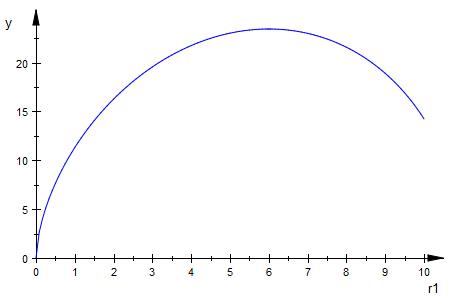
r1 = 6
r2 = ( 44 - 4 * r1 ) / 5
r2 = ( 44 - 4 * 6 ) / 5
r2 = 4

f(r1 ; r2)= 4 r1^0,5 r2^0,6

f( 6 ; 4 )= 4 * 6^0,5 * 4^0,6
f = 4 * 2.45 * 2.30
f = 22.51

zu b.) kann ich eh nichts sagen.

Ich hoffe ich konnte dir weiterhelfen.