wenn du dir eine Skizze vom Turm und dem Boden darunter samt Wurfbahn machst, dann wirst du schnell sehen, dass du es mit der Bahngleichung eines waagerechten Wurfs zu tun hast. Die Gleichung für eine solche Wurfbahn lautet:
$$ y=\frac { g }{ 2v_0^2 }x^2 $$
Da g und v0 konstant sind, hast du es mit einer Parabel (wegen x2) zu tun. Die Wurfbahn setzt sich eigentlich aus zwei unterschiedlichen Bewegungen zusammen: Es hilft, wenn man sie sich erstmal unabhängig voneinander vorstellt.
Die erste ist die reine Bewegung nach unten: Stell dir vor, du lässt den Stein einfach senkrecht vom Turm fallen. Die Erdbeschleunigung ist das einzige, was auf ihn wirkt. Er fällt also direkt nach unten und hört nicht eher auf, bis er den Boden erreicht. Seine Geschwindigkeit ist in diesem Fall v=gt.
Die zweite ist die reine Bewegung vom Turm weg: Stell dir vor du stehst auf dem Turm aber du stehst im Vakuum und es gibt keine Erdbeschleunigung mehr. Wirfst du nun den Stein von dir mit der Geschwindigkeit v0 so fliegt er für immer so weiter ohne sich jemals nach unten zu krümmen oder sonstwie von der Bewegungsgerade abzuweichen. Das entspricht auch fast genau der Art und Weise, wie sich Dinge im Weltraum auch bewegen. Die Geschwindigkeit des Steins ist in diesem Fall für immer und ewig die Geschwindigkeit, mit der du ihn geworfen hast: v=v0.
Nun stell dir diese beiden Bewegungen als Pfeile vor, unabhängig voneinander. Wenn du sie zusammenaddierst, dann zeigen sie in jene gemeinsame Richtung, die dein Stein einschlägt, wenn du ihn auf der Erde mit Schwerkraft wirfst:
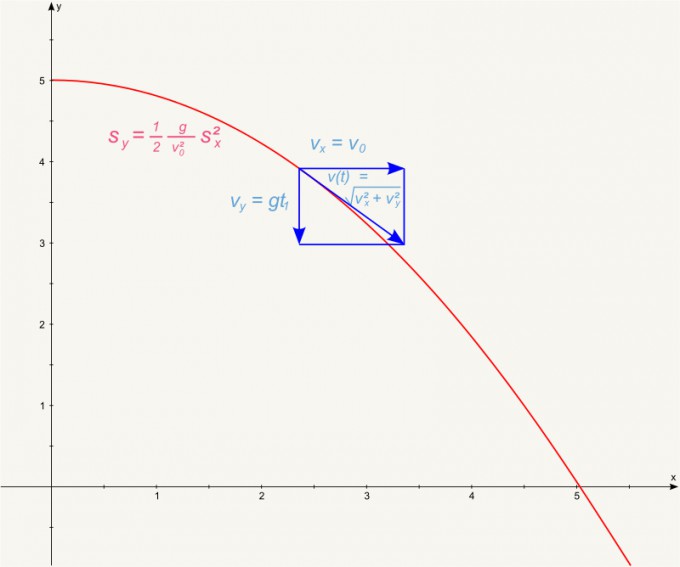
In diesem Bild ist die y-Achse zwar nach oben gerichtet, aber ich würde dir empfehlen, deine eigene nach unten zu richten. Das macht die Rechnerei etwas einfacher, denn du musst so nicht mit Minusvorzeichen bei der eingeschlagenen Höhe arbeiten.
Um nun mit 1) anzufangen, brauchst du nur die Wurfbahngleichung nach v0 umzustellen und sie auszurechnen. Denn die durchfallene Höhe (62m) und die x-Stelle (44m) hast du bereits schon.
Du erhältst damit eine Anfangsgeschwindigkeit von
$$ v_0=\sqrt { \frac { g\cdot1936m^2 }{ 2*62m } }\approx12,4\frac { m }{ s } $$
Um die Endgeschwindigkeit zu berechnen kannst du das obige Bild zuhilfe nehmen: Du musst nämlich die resultierende Geschwindigkeit berechnen für den Zeitpunkt, zu dem der Stein auf den Boden knallt. Diese Gleichung ist
$$ v(t)=\sqrt { v_0^2+(gt)^2 } $$
Dir fehlt aber erstmal die Zeit. Diese bekommst du aber aus der Gleichung für die durchfallene Höhe. Diese lautet nämlich
$$ h=\frac {gt^2 }{ 2 }$$
Du weißt, dass dein Stein 62m gefallen ist, also setzt du ein und löst nach t auf, wobei du bekommst:
$$ t=\sqrt { \frac { 2h }{ g } }=\sqrt { \frac { 2\cdot62m }{ 9,81\frac { m }{ s^2 } } }\approx 3,5s$$
Der Stein schlägt also nach 3,5 s am Boden auf. Diese Zeitangabe kannst du nun einsetzen, um endlich die Endgeschwindigkeit auszurechnen. Diese ist:
$$ v(3,5s)=\sqrt { v_0^2+(g(3,5~s))^2 }=\sqrt { (12,4~m/s)^2+(9,81~m/s^2\cdot3,5~s)^2 }\approx36,5\frac { m }{ s } $$
Zu 2)
Lege den Ursprung deines Koordinatensystems am besten oben links. Die y-Achse sollte senkrecht davon nach unten, die x-Achse nach rechts davon. Die Bahn sollte sich nach unten hin krümmen und nicht weiterführen als 44m an der x-Achse. In etwa so:
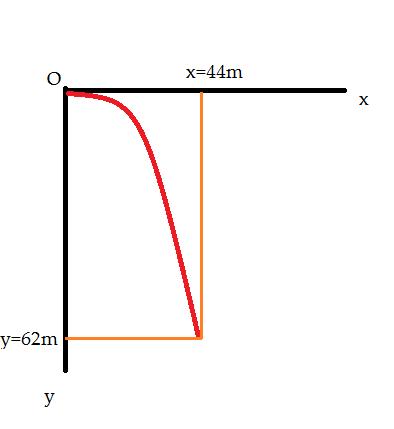
Zu 3)
Die "Bewegungsrichtung" ist der Geschwindigkeitsvektor des Steins beim Auftreffen. Wie gesagt: Diese ist die Summe des senkrechten Geschwindigkeitsvektors in y-Richtung
$$ \vec v_y=\vec g(t)$$
und des waagerechten Vektors in x-Richtung
$$ \vec v_x=\vec v_0$$
Falls du das nicht ganz verstehst, sieh dir nochmal das erste Bild oben an.
Die Bewegungsrichtung zum Zeitpunkt des Auftreffens ist also der resultierende Geschwindigkeitsvektor des Steins zum Zeitpunkt t=3,5s. Er ist
$$ \vec v(3,5~s)=\vec v_x+\vec v_y(3,5~s)=\vec v_0+\vec g(3,5~s)=\begin{pmatrix} 12,4~m/s\\9,81~m/s^2\cdot3,5~s\\\end{pmatrix}=\begin{pmatrix} 12,4~m/s\\34,3~m/s\\ \end{pmatrix} $$
Wichtig ist die Vektorschreibweise hier, weil nur sie eine "Richtung" angeben kann und gefragt war eben die Bewegungsrichtung.
Ich hoffe, ich konnte dir helfen. Solltest du Fragen haben, dann kommentiere einfach meine Erklärung, damit ich es per Mail mitbekomme. Ich wünsche noch viel Freude bei der Physik!