Auf einem 26m hohen Turm wird ein Stein im Punkt T unter dem Winkel A in die Luft geworfen.

Question

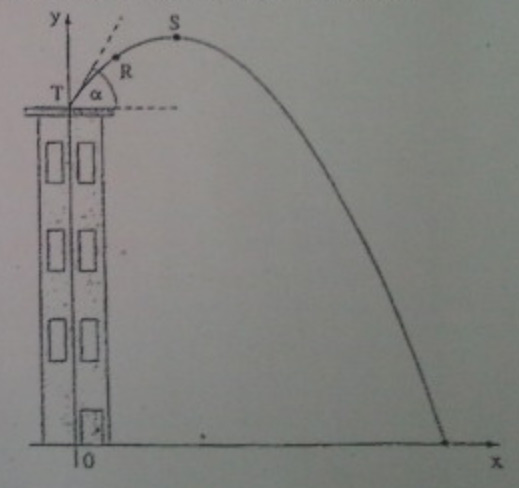
Aufgabe:

Auf einem \( 26 \mathrm{~m} \) hohen Turm wird ein Stein im Punkt T unter einem Winkel α in die Luft geworfen. Dabei erreicht er nach kurzer Zeit den Punkt R(10 | 36). Die Koordinaten sind in Meter angegeben.

a) Bestimmen Sie aus den Angaben eine quadratische Funktion, wenn gelten soll:
\( f(x)=-x^{2}+b x+c \)

b) Berechnen Sie in welcher Entfernung vom Turm der Stein auf den Boden aufschlägt.

c) Bestimmen Sie die maximale Höhe des Steins.

d) Bei \( \mathrm{x}=12 \) steht ein \( 13 \mathrm{~m} \) hoher Fahnenmast. Ermitteln Sie rechnerisch ob der Stein den Mast bei seinem Flug triff. [Kontrollergebnis: \( f(x)=-x^{2}+11 x+26 \)]

Comments

2 Gleichungen sollten bei a) genügen, da du ja nur b und c bestimmen musst.

---

sind die Punkte P1 (10/36) und P2 (0/26) ausreichend?

---

Ja. Das sollte so sein. Denn aus 2 Punkten bekommst du 2 Gleichungen.

---

so ok?

I 36=-100+10+c
II 26=0+0+c

Answer 1

I 36=-100+10b+c
II 26=0+0+c

II -----> c=26 

in I einsetzen

36 = - 100 + 10b + 26

36 - 26 + 100 = 10b

110 = 10b

11 = b

y = -x^2 + 11x + 26

Comments

b)  -x² + 11x + 26 = 0       abc oder pq-Formel verwenden und die positive Lösung wählen.

c) Scheitelpunktform der Parabelgleichung erstellen

y = -x² + 11x + 26

 = -(x² - 11x - 26)

= -((x -5.5)^2 - 5.5^2 - 26)

= -(x-5.5)^2 + 56.25

S(5.5 | 56.25) 

Kontrolle: Graph

d) x= 12 einsetzen:

y = -x² + 11x + 26 = -144 + 132 + 26 = 14 

Der Stein hat an der Stelle x=12 noch die Höhe 14m über Grund. Daher trifft er den Fahnenmast nicht.

---

bei b) muss ich durch -1 rechnen ja?

---

Ja, wenn du die pq-Formel benutzen willst. Sonst kannst du einfach a = - 1 wählen.

b)  x² - 11x - 26 = 0     

x1,2 = 5.5 ± √(5.5^2 + 26) 

x1 = 13

x2 = - 2 (real uninteressant)

---

Lu kannst du den titel meiner frage umformen?