Aufgabe 17 - Schrittkreis von zwei Kugeln:
In den Bildern ist die Lage von zwei Kugeln zueinander dargestellt.

Der interessante Fall ist der, wenn die beiden Kugein einen Schnittkreis haben.
Eine Kugel mit Mittelpunkt \( (-2|-2| 1) \) hat den Radius 4, die zweite Kugel hat den Mttelpunkt \( (-1|3| 3) \) und den Radius 3. Bestimmen Sie die Gleichung der Ebene, in der die gemeinsamen Punkte der beiden Kugeln liegen, und bestimmen Sie den Mittelpunkt und den Radius des Schnittkreises.
Zeichnen Sie beide Kugeln und die Ebene.
Ebene eines Schnittkreises Da die gemeinsamen Punkte beide Kugelgleichungen erfüllen, genügen sie auch jeder Kombination der
Gleichungen. Multiplizieren Sie beide Gleichungen aus.
Zum Beispiel werden die beiden Kugelgleichungen
\( K_{1}:\left(x_{1}+3\right)^{2}+{x_{2}}^{2}+\left(x_{3}+2\right)^{2}=25 \) und
\( K_{2}:\left(x_{1}+2\right)^{2}+\left(x_{2}-1\right)^{2}+{x_{2}}^{2}=49 \)
vereinfacht zu
\( K_{1}: {x_{1}}^{2}+6 x_{1}+{x_{2}}^{2}+x_{3}^{2}+4 x_{3}=12 \) und
\( K_{2}: {x_{1}}^{2}+4 x_{1}+{x_{2}}^{2}-2 x_{2}+{x_{3}}^{2}=44 \)
Die Differenz "linke Seite minus linke Seite ..." ergibt:
\( 2 x_{1}+2 x_{2}+4 x_{1}=-32 \) ist die Gleichung der Ebene, die den Schnittkreis enthält.
Durch Subtraktion ("linke Seite minus linke Seite, rechte ...") werden die quadratischen Terme eliminiert. Der Rest ist die Gleichung einer Ebene.
Aufgabe 18 - Kugel in einer Pyramide:
Eine quadratische Pyramide hat die Grund. kante 40 und die Höhe 60. Die Grundkanten sind parallel zur \( x_{1} \) - und zur \( x_{2} \)-Achse, die Spitze liegt auf der \( x_{r} \) Achse. Berechnen Sie den Radius del grṓbten Kugel, die gerade noch in die Pyramide hineinpasst und zeichnen Sie die Pyramide mit der Kugel.
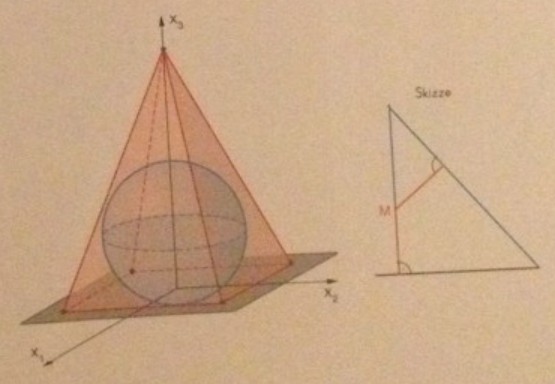
Tipp: Der Mittelpunkt liegt auf der Höhe der Pyramide und hat zu den Seitenflächen denselben Abstand wie zur Grundfläche.