Eingesperrtes Rechteck zwischen Graph von f(x) = 1 + 4/x^2 und Achsen. Minimaler Flächeninhalt des Rechtecks.

Question

Aufgabe Eingespertes Rechteck:

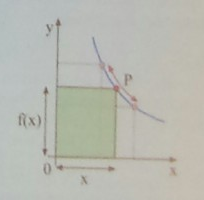
Zwischen Ursprung und Graph der Funktion \( f(x)=1+\frac{4}{x^{2}} \) ist wie abgebildet ein achsenparalleles Rechteck eingesperrt. Eine Ecke des Rechtecks ist der Ursprung, die gegenüberliegende Ecke P liegt auf dem Graphen von f.

Wie müssen die Koordinaten von P gewöhlt werden, damit der Flächeninhalt des Rechtecks minimal wird?

Answer 1

P hat die Koordinaten  ( x ;  1+4/x^2 )
Also Fläche
A(x) = x * f(x) =  x + 4/x    und   A ' (x) =  1 - 4/x^2 
Damit A ' (x) = 0 für   x=2 denn es muss x>0 sein.

A ' ' (x) =  8/ x^3 also  A ' ' ( 2) = 1 > 0, also Min von A(x) bei x=2.
Damit muss P ( 2 /  2) sein.

Comments

Was ist di Nebenbedingung bei der Aufgabe ich brauche dringend Hilfe.

Mathe-verzweifelft

---

Nebenbedingung f(x)= 1/x .

Flächenformel A(x) = x*f(x) .

---

Ich verstehe das irgendwie nicht muss die nebenbedingung nicht 2 variablen beinhalten?

Mathe-verzweifelt

---

Mit f(x)=y hast du y = 1+4/x^2 und A= A(x,y) = x*y

---

Danke damit hast du mir grade sehr geholfen