Extremwertaufgabe: Überprüfen einer Aussage zu f(x)= 2x^2 - 5x - 3

Question

Ich brauch mal eure Hilfe,

K_f   ist das Schaubild der Funktion f f(x)= 2x² -5x-3.

a) Die Gerade mit der Gleichung x=u schneidet die x-Achse im Punkt Q und das Schaubild K_f im Punkt P. Für 0<u<3 sind die Punkte P,Q, und S(3/0) die Eckpunkte eines Dreiecks.

Der Flächeninhalt des Dreiecks wird am größten für u=0,6. Überprüfen Sie diese Behauptung.

b) Berechnen Sie a [0;2], so dass die Punkte C und D den größten Abstand haben. (vgl. Abb.3)

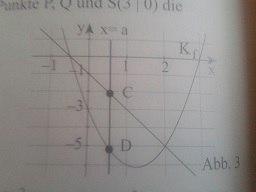
Danke für Eure Hilfe :))

Answer 1

a)

A = 1/2 · (3 - x) · (2·x^2 - 5·x - 3) = - x^3 + 5.5·x^2 - 6·x - 4.5

A' = - 3·x^2 + 11·x - 6 = 0 --> x = 2/3

u sollte 2/3 sein und nicht 0.6

b)

d = (- 2·x - 1) - (2·x^2 - 5·x - 3) = - 2·x^2 + 3·x + 2

d' = 3 - 4·x = 0 --> x = 3/4

a = 3/4 = 0.75