Hi,
betrachte das Lagrange Restglied das wie folgt aussieht
$$ R_n f(x;a) = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-a)^{n+1} $$ mit $$ \xi \in [a,x] $$
Setzte \( f(x) = cos(x) \), \( x = \frac{1}{2} \) und \( a = 0 \)
Die Ableitung des Kosinus ergibt entweder einen Sinus oder wieder einen Kosinus, s.d. man das Restglied wie folgt abschätzten kann
$$ \left| R_n f\left(\frac{1}{2};0\right) \right| \le \left| \frac{\left(\frac{1}{2}\right)^{n+1}}{(n+1)!} \right| $$
Das Restglied muss jetzt kleiner als \( 0.0001 \) sein, also muss gelten $$ \left| \frac{\left(\frac{1}{2}\right)^{n+1}}{(n+1)!} \right| \le 0.0001 $$
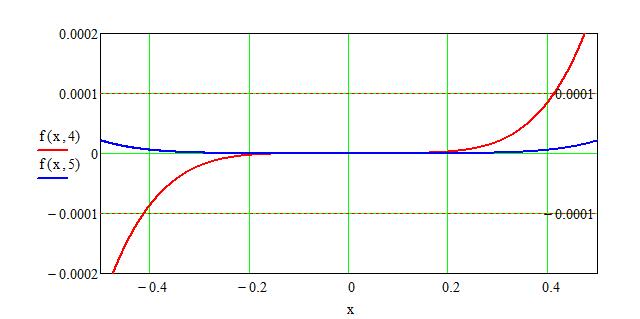
Das ist eine Ungleichung die nur noch von \( n \) abhängt. Durch ausrechnen erhält man, dass das kleinste \( n \), dass die Ungleichung erfüllt \( n = 5 \) ist, was man auch an der Grafik erkennen kann.