1.) Vom künstlich in Kernreaktoren hergestellten Plutonium gibt es mehrere unterschiedlich langlebige Isotope. Das Plutonium-Isotop240Pu hat die Halbwertszeit tk=6600 Jahre.
a) Bestimme die Zerfallskonstante aus der Halbwertszeit und erstelle damit den Term der Zerfallsfunktion N(t), wobei gilt N0=100 (in g).
0.5^{1/6600} = e^ 1/6600*ln(0.5) = -1.050 * 10-4
N(t) = 100*0.5^{t/6600} = 100*e^{-0.0001050t}
b) Zeichne den Graphen der Zerfallsfunktion im Zeitraum zwischen 0 und 25000 Jahren.
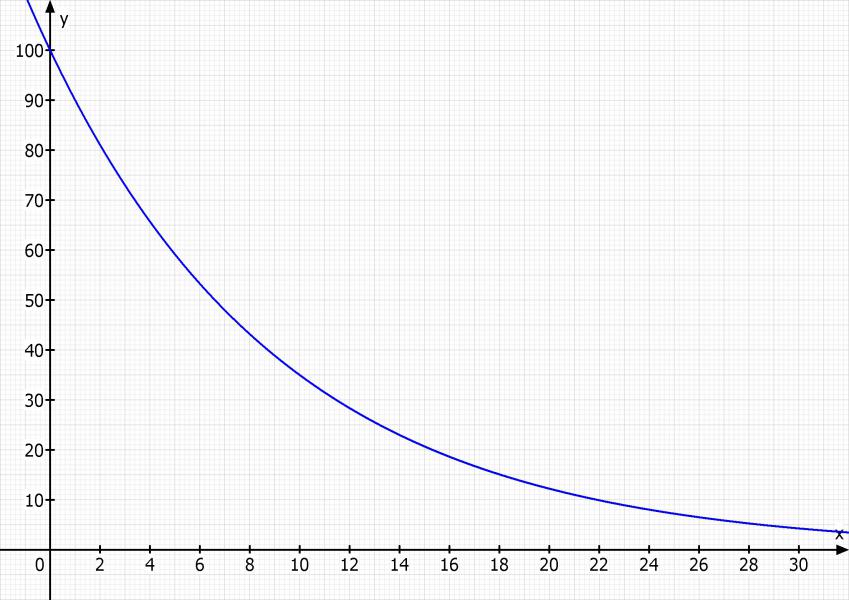
x-Achse in 1000 Jahre
c) Berechne, wann nur noch weniger als 1%0 (=0,1%) der Ausgangsmenge vorhanden ist.
0.5^{t/6600} < 0.001
t > 65774.1 Jahre
d) Begründe, dass die Zerfallsgeschwindigkeit durch die Ableitung N`(t) gegeben ist.
Die Ableitung N' ist ein Maß für die Abnahme in einer Bestimmten Zeit und damit eine Geschwindigkeit.
e) Berechne die Zerfallsgeschwindigkeit nach 1000 Jahren. t ist die Zeit N(t) ist die Menge zur Zeit t N0 ist die Menge zur Zeit 0 k ist eine stoffspezifische Zerfallskonstante
N(t) = 100*0.5^{t/6600}
N'(t) = 100/6600·0.5^{t/6600}·LN(0.5)
N'(1000) = -0.009455
Für Hilfe wäre ich unglaublich Dankbar. Es würde auch reichen, wenn ihr mir die allgemeinen Formeln sagen könnt, wie ich zum Beispiel k oder t berechne. Lg und vielen Dank schon Mal