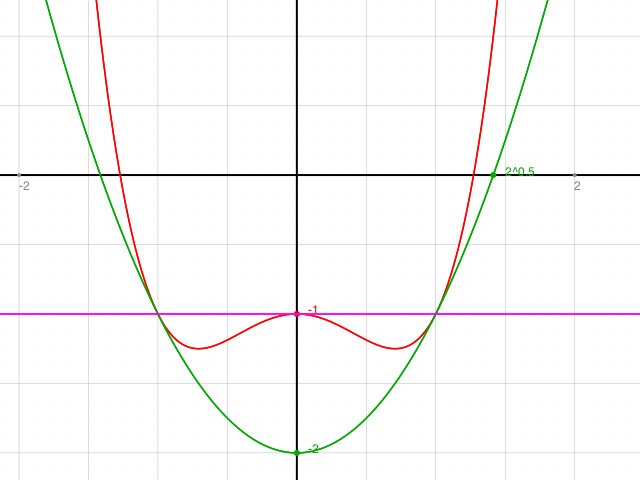
Das Schaubild K einer Parabel 4 Ordnung hat in H(0/-1) ein maximum und verläuft symmetrisch zur ordinate. K und der Graph g der parabel g(x)=x2-2 berühren sich für x=1.
Symmetrie: Ansatz
f(x) = ax^4 + bx^2 + c
f ' (x) = 4ax^3 + 2bx
H ---> c = -1
Graph g der parabel g(x)=x2-2 berühren sich für x=1.
g'(x) = 2x
g'(1) = 2 ==> f'(1) = 2 (I)
g(1) = 1-2 = -1 ==> f(1) = -1 (II)
Ansatz mit c = -1 in (I) und (II) einsetzen. --> a und b bestimmen.
g'(1) = 2 ==> f'(1) = 2 (I) 4a + 2b = 2
g(1) = 1-2 = -1 ==> f(1) = -1 (II) a + b - 1 = -1. ---> a+b = 0, a = -b
in (I)
4(-b) + 2b = 2
-2b = 2 ---> b = -1. Wegen (I) ---> a = 1.
f(x) = x^4 - x^2 - 1.
Kontrolle f und g mit Funktionsplotter: