Reichen 10 Liter Farbe für ein Vereinslogo aus?

Question

Aufgabe Vereinslogo:

Der Marineclub erhält ein neues 5 m langes Vereinslogo in Form eines stilisierten Walfisches.

Es soll beidseitig mit Zinkfarbe gestrichen werden, um es wetterfest zu machen. Der Anstrich soll mindestens 1 mm dick sein.

Reichen 10 Liter Farbe aus?

Hinweis: Zeigen Sie zunächst, dass die Schwanzflosse des Logos 1 m lang ist.

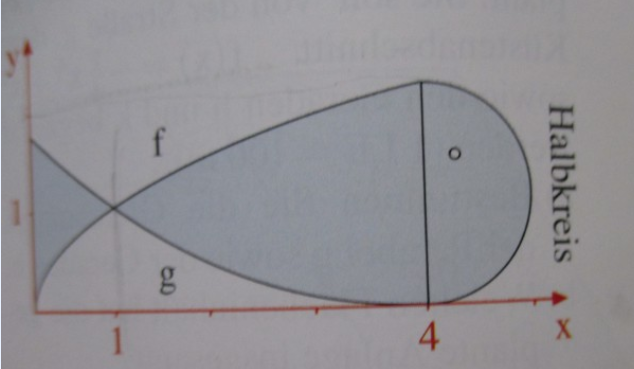
\( f(x)=\sqrt{x}, 0 \leqslant x \leqslant 4 \)

\( g(x)=\frac{1}{9}\left(x^{2}-8 x+16\right), 0 \leqslant x \leqslant 4 \)

Ansatz/Problem:

Ich weiß, dass ich die Fläche berechnen muss, aber ich weiß nicht ob ich erst vom Intervall 0-1 und dann 1-4 oder gleich 0-4 berechnen soll... und dann muss ich das ganze nur mal 1 mm rechnen oder?

~plot~ (x>=0)*(sqrt(x))*(x<=4);(x>=0)*(1/9(x^2-8x+16))*(x<=4);[[-1|5|-1|3]] ~plot~

Comments

Vom Duplikat:

Titel: Vereinslogo: Reichen 10 Liter Farbe aus?

Stichworte: fläche,flächeninhalt,bruchgleichung,quadratische-gleichungen

Aufgabe:

Der Marineclub erhält ein neues 5m langes Vereinslogo in Form eines stilisierten Wals. Er soll beidseitig mit Zinkfarbe gestrichen werden. Der Anstrich soll mindestens 1mm dick sein. Reichen 10 Liter Farbe aus? Hinweis: zeigen sie zunächst, dass die Schwanzflosse des Logos 1m lang ist.

F(x)=-1/6x^2+7/6x,  0≤x≤4

G(x)=1/9(x^2-8x+16), 0≤x≤4

Also als erstes muss ich doch die die Schnittpunkte berechnen und dan die Differentialgleichung?

---

Was mir so spontan einfällt dazu:

1.

zeigen sie zunächst, dass die Schwanzflosse des Logos 1m lang ist.

Das ist auf der Skizze bereits so eingezeichnet.

2.

Jede Anstreichfarbe enthält ein Lösungsmittel, und sei das nur Wasser. Das Lösungsmittel verdunstet beim Trocknen weitgehend. Wenn die Farbdicke 1 mm sein soll, müsste man das Verdunsten berücksichtigen, denn dieser Anteil der Farbe ist dann weg. Ich gehe davon aus, dass soll ignoriert werden.

3.

Wenn das Logo z.B. aus einem Brett ausgeschnitten wird, müssten die Stirnseiten wahrscheinlich auch 1 mm dick mit (eingetrockneter) Farbe bedeckt sein. Die Bogenlängen könnte man ja berechnen, aber es fehlt die Dicke des Bretts. Ich gehe davon aus, auch dass soll ignoriert werden. Zumal die Konstruktion beim Ausschneiden ja auch nicht stabil wäre, die Schwanzflosse würde abfallen.

---

Vom Duplikat:

Titel: Zeigen Sie zunächst,dass die Schwanzflosse des Logos 1m lang ist.

Stichworte: modellieren

Aufgabe:

Der Marineclub erhält ein neues 5m langes Vereinslogo in Form eines stilisierten Wals.Es soll beideseitig mit Zinkfarbe gestrichen werden,um es wetterfest zu machen.Der Anstrich soll mindestens 1mm dick sein.Reichen 10 Liter Farbe aus?

Zeigen Sie zunächst,dass die Schwanzflosse des Logos 1m lang ist.

Problem/Ansatz:

Kann jemand helfen?Als Erstes habe ich den Schnittpunkt und dann die Differensfunktion ausgerechnet.Dann habe ich den Flächeninhalt im Intervall 0 bis 1 und 1-4 ausgerechnet.Weiss jetzt net weiter.

0-1: 91/108

1-4:4,25

---

Vom Duplikat:

Titel: Reichen 10 Liter Farbe aus?

Stichworte: modellieren

Aufgabe:

Der Marineclub erhält ein neues 5m langes Vereinslogo in Form eines stilisierten Wals.Es soll beideseitig mit Zinkfarbe gestrichen werden,um es wetterfest zu machen.Der Anstrich soll mindestens 1mm dick sein.Reichen 10 Liter Farbe aus?

Zeigen Sie zunächst,dass die Schwanzflosse des Logos 1m lang ist.

…

Problem/Ansatz:

Kann jemand helfen?Als Erstes habe ich den Schnittpunkt und dann die Differensfunktion ausgerechnet.Dann habe ich den Flächeninhalt im Intervall 0 bis 1 und 1-4 ausgerechnet.Weiss jetzt net weiter.

0-1: 91/108

1-4:4,25

---

Wenn derselbe Benutzer dieselbe Frage an demselben Abend zweimal stellt, ist das kontraproduktiv.

Answer 1

Zuerst den Schnittpunkt berechen
f ( x ) = g ( x )
Es soll x = 1 herauskommen

Dann die Differenzfunktion
f - g
bilden und davon die Stammfunktion erstellen
Dann von 0 bis und 1 bis 4 getrennt berechnen
und die absolut-Beträge addieren.

Nun noch den Funktionswert von f ( 4 )
ermitteln ( g ( 4 ) ist wohl 0 )
und den Halbkreis berechnen.

Das ist die Fläche.
Fläche mal Höhe ergint das Volumen.
Darauf achten das die Einheiten gleich sind.

mfg Georg

Die Lösung stelle ich noch hier ein.

Comments

Es müßte für alle 3 Flächen 5.94 m^2 herauskommen.
V = 594 dm^2 * 0.01 dm
V = 5.94 dm^3 = 5.94 Liter

Alle Angaben ohne Gewähr.

mfg Georg

Answer 2

Flächeninhalt A = \( \int\limits_{0}^{1} g(x) - f(x) \ dx \) + \( \int\limits_{1}^{4} f(x) - g(x) \ dx \) + \( \frac{1}{2} \) π r²

wobei r = f(4) / 2

Das ist für eine Seite des Wals.

Answer 3

Da fehlt doch nur noch der Halbkreis, der hat den

Durchmesser f(4).