Gleichschenkliges Dreieck: Berechne nacheinander x, y und c (Trigonometrie)

Question

Aufgabe:

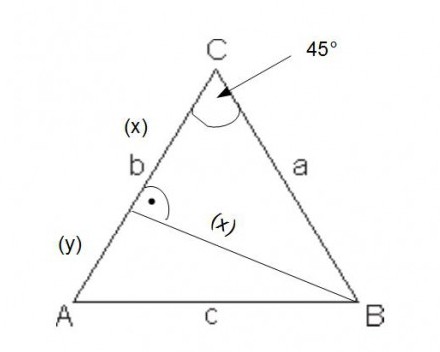
\( \mathrm{ABC} \) ist ein gleichschenkliges Dreieck mit (Gamma \( 45^{\circ} \) ) Und \( \mathrm{CA}=\mathrm{CB}=10 \mathrm{~cm} \).

a) Berechne nacheinander \( \mathrm{x}, \mathrm{y} \) und \( \mathrm{c} \).

b) Berechne anschließend \( \sin 22,5^{\circ}, \cos 22,5^{\circ} \) und \( \tan 22,5^{\circ} \).

Nun zu meiner Frage:

Also ich habe die Nummer a) berechnet, bei der b) allerdings Komme ich nicht weiter, da ich nicht verstehe, was bzw. wie ich es berechnen soll.

Answer 1

Zeichne dir doch mal die Winkelhalbierende von gamma ein.
Das ist zugleich auch die Höhe h_c , weil das Dreieck gleichschenklig ist.
Und die trifft auch unten in der Mitte der Seite c auf, sagen wir mal bei M.

Dann ist AMC einrechtwinkliges (wegn Höhe) Dreieck mit
Hypotenuse b und den Katheten h und c/2
Wenn du c berechnest hast, hast du ja auch c/2
und b war ja gegeben : 10cm.

Und dann ist sin(22,5°) = Gegenkath / Hypotenuse =  c/2  /  b

etc.