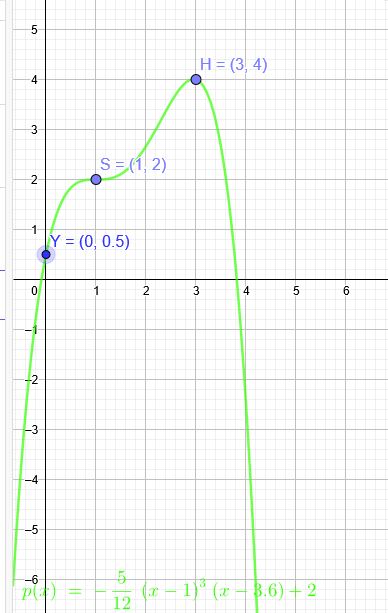
Ich bestimme die ungefähre Funktion:
Sattelpunkt bei \(S(1|\red{2})\) Hochpunkt bei \(H(3|4)\)
Ich verschiebe den Graph um \(\red{2} \)Einheiten nach unten:
\(S´(1|0)\) Hier ist nun eine dreifache Nullstelle.
\(f(x)=a(x-1)^3(x-N)\)
\(H´(3|2)\)
\(f(3)=a(3-1)^3(3-N)=8a(3-N)\)
\(8a(3-N)=2\) → \(4a(3-N)=1\) → \(a=\frac{1}{12-4N}\)
\(f(x)=\frac{1}{12-4N}(x-1)^3(x-N)\)
Schnitt mit der y-Achse ≈ bei \(Y(0|-1,5)\)
\(f(0)=\frac{1}{12-4N}(0-1)^3(0-N)=\frac{N}{12-4N}\)
\(\frac{N}{12-4N}=-1,5\)
\(\frac{N}{12-4N}=-1,5\)
\(N ≈3,6\) \(a≈\frac{1}{12-4\cdot 3,6}=-\frac{5}{12}\)
\(f(x)=-\frac{5}{12}(x-1)^3(x-3,6)\)
Nun 2 Einheiten nach oben:
\(p(x)=-\frac{5}{12}(x-1)^3(x-3,6)+2\)
Es handelt sich hier um ein Polynom 4.Grades.