Zuerst ergänzt du die fehlenden Winkel:
1. 180° - 40° = 140° (an Punkt B, gestreckter Winkel ist 180°)
2. 180° = 25° + 140° + 15° (Innenwinkelsummensatz)
3. 180° = 40° + 90° + 50° (Innenwinkelsummensatz)
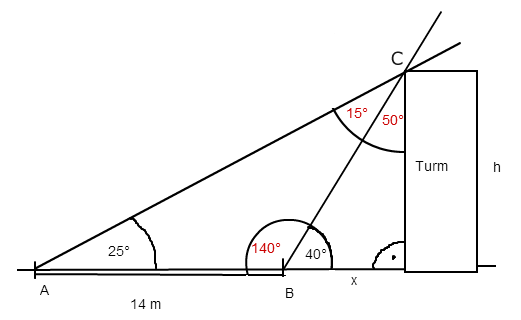
Anschließend berechnest du über den Sinussatz die Strecke BC:
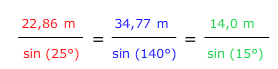
Jetzt weißt du, dass BC ≈ 22,86 m lang ist.
Da das kleine Dreieck rechtwinklig ist, können wir jetzt die Strecke BC als Hypotenuse nutzen und mittels Kosinus die Länge x berechnen:
cos(40°) = AK / HY
cos(40°) = x / 22,86 m |* 22,86 m
cos(40°) * 22,86 m = x
x = cos(40°) * 22,86 m
x ≈ 17,5118 m
Solltest du dich mit Sinus und Kosinus noch nicht auskennen, siehe:
Und hier findest du wesentliche Informationen über den Sinussatz und den Kosinussatz, nutze auch die Programme dort, um weitere Aufgaben zu lösen:
https://www.matheretter.de/wiki/kosinussatz